9th Class Mathematics Triangles Triangles

Triangles

• A triangle is a closed figure bounded by three straight lines. It is denoted by the symbol\[\Delta \].

\[\Delta \]ABC has three sides denoted by AB, BC and CA; three angles denoted by \[\angle ~A,\angle B\text{ }and\text{ }\angle C\,;\]and three vertices denoted by A, B and C.

• Two geometrical figures are said to be congruent if they have exactly the same shape and size. Congruence is denoted by the symbol =.
• Two triangles are congruent if the sides and angles of one triangle are equal to the corresponding sides and angles of the other triangle.

• The congruence of two triangles ABC and PQR under the correspondence \[A\leftrightarrow P,B\leftrightarrow Q\]

and \[C\leftrightarrow R\]is symbolically expressed as \[\Delta ABC=\Delta PQR.\]

• Two congruent figures are equal in area, but two figures having the same area need not be congruent.

• Congruence relation is an equivalence relation:

(i) Congruence relation is reflexive.

\[\Delta ABC=\Delta ABC.\]

(ii) Congruence relation is symmetric.

If \[\Delta ABC\text{ }\cong \text{ }\Delta DEF,\text{ }then\text{ }\Delta DEF\text{ }\cong \text{ }ABC\text{ }.\]

(iii)Congruence relation is transitive.

• If \[\Delta ABC\text{ }=\text{ }\Delta DEF\text{ }and\text{ }\Delta DEF\text{ }=\text{ }\Delta XYZ\text{ }then\text{ }\Delta ABC\text{ }=\text{ }\Delta XYZ.\]
• Criteria for congruence of triangles:

• (i) A.S. congruence rule: Two triangles are congruent if two sides and the included angle of

one triangle are equal to the two sides and the included angle of the other triangle.

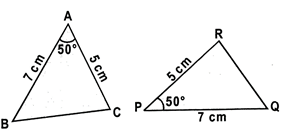
\[\Delta ABC=\Delta PQR\]

\[Since=PQ=7cm,\text{ }\angle C=PR=5cm\,\,and\,\angle A=\angle P=50{}^\circ .\]corresponding sides and angles of the other triangle.

(ii) A.S.A. congruence rule: Two e.g., triangles are congruent if two angles and the included side of one triangle are equal to two   angles and the included side of the other triangle.

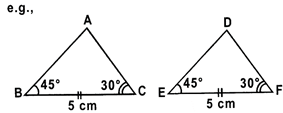
\[\Delta ABC\cong \Delta DEF\]

\[\angle B=\angle E={{45}^{o}},\angle C=\angle F=30{}^\circ \text{ }and\text{ }BC\text{ }=\text{ }EF\text{ }=\text{ }5cm.\]

(iii) S.S.S. congruence rule: If three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.                    

\[\Delta ABC=\Delta XYZ\]

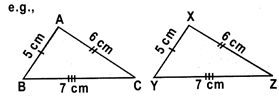
Since AB = XY = 5 cm, BC = YZ = 7 cm and CA = ZX = 6 cm.

• H.S.congruencerule: fin two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent.

Right angle - Hypotenuse

\[\Delta ABC=\Delta PQR\]

Since \[\angle \]B =\[\angle \]Q = 90°, AC = PR = 5 cm and AB = PQ = 4 cm.

(v) A.A.S. or S.S.A. congruence rule: Two

triangles are congruent if any two pairs of angles and one pair of corresponding sides are equal.        

\[\Delta ABC.\text{ }\Delta DEF\]                      
                  

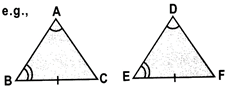
Since \[\angle \]A = \[\angle \]D, \[\angle \]B = \[\angle \]E and BC = EF.

• Inequalities in a triangle:

(i) If two sides of a triangle are unequal, then the angle opposite to the longer side is greater than that opposite to the shorter side.

• Note: In any triangle, the side opposite to the larger angle is longer.

(ii) In a right triangle, hypotenuse is longer than the other two sides.

(iii) The sum of any two sides of a triangle is greater than the third side.

(iv) An exterior angle of a triangle is greater than either of its interior angles.