Acceleration Due to Gravity
Category : 9th Class
Acceleration Due To Gravity
Let us consider al ball dropped from a certain height. As the ball falls towards the ground its velocity increases.
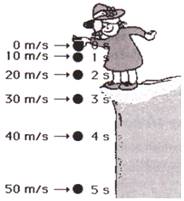
Let 'm' be the mass of the ball falling from a certain height freely under the influence of gravity. Then the force between the ball and the earth is given by
\[F=G\,\frac{m\times {{M}_{e}}}{R_{e}^{2}}\] …………. (1)
Where, \[{{M}_{e}}\] is the mass of the earth
\[{{R}_{e}}\] is the radius of the earth
During the fall there is no change in direction but there will be continuous change in velocity. Hence the object will be falling towards the earth with an acceleration due to the earth's gravitational force. This acceleration is called the acceleration due to the gravity. It is denoted by 'g'. Thus, force due to earth's gravity is given by
\[\mathbf{F=m\times g}\]……………. (2)
From equation (1) and (2) we have
\[m\times g=G\frac{m\times {{M}_{e}}}{R_{e}^{2}}\]
\[g=G\,\frac{{{M}_{e}}}{{{R}_{e}}^{2}}\]
Therefore, we see that acceleration due to gravity is independent of mass of the object. On putting the value we get the value of g=9.8m/s2 approximately. Since the earth is not perfectly spherical, the radius of earth increases from pole to the equator, hence the value of g decreases from the pole to the equator.
Equation of Motion Falling Freely under Gravity
We have three equations of motion, which describes the motion of the bodies on the surface of the earth. The three equations of motions are
\[v=u+at;\,\,s=ut+\frac{1}{2}\,a{{t}^{2}}\] and \[{{v}^{2}}={{u}^{2}}+2as\]
Motion of the object under the influence of gravity is such that the object will either fall towards the earth or will go up against the gravity. When the object falls towards the earth surface then g is positive and when it is thrown upward then g is negative. Hence in such cases we have a = +g or -g accordingly. The equations of motion under the influence of gravity is thus reduced to
\[v=u+gt\,;\,\,h=ut+\frac{1}{2}g{{t}^{2}}\] and \[{{v}^{2}}={{u}^{2}}+2gh\]
Mass and Weight
Mass of a body is defined as the total quantity of matter contained in the body. It can also be defined as the measure of inertia. We can, therefore, say that mass of the object remains the same everywhere in this universe. The weight of an object is defined as the force with which an object is attracted towards the centre of the earth. The relation between mass and weight can be reduced as follows. Let W be the weight of an object of mass 'm' on the earth/then
\[W=G=\frac{m\times {{M}_{e}}}{{{R}_{e}}^{2}}\]
Or, \[W=m\times \,\left( G\,\frac{{{M}_{e}}}{{{R}_{e}}^{2}} \right)\]
Or, \[W=m\times g,\] where \[g=\,\left( G\,\frac{{{M}_{e}}}{{{R}_{e}}^{2}} \right)\]
Weight of the Object on the Moon
Let \[{{M}_{m}}\] be the mass of the moon and \[{{R}_{m}}\], be the radius of the moon. Let us consider an object of mass 'm' be placed on the surface of the moon, then the weight of the object on the surface is given by
\[{{W}_{m}}=G\,\frac{{{M}_{m}}\times m}{{{R}_{m}}^{2}}\] ………..(1)
But/ the weight of same object on the surface of earth is given by
\[{{W}_{e}}=G\,\frac{{{M}_{e}}\times m}{{{R}_{e}}^{2}}\] ………..(2)
No taking the ratio we get,
\[\frac{{{W}_{m}}}{{{W}_{e}}}=\frac{G\frac{{{M}_{m}}\times m}{{{R}_{m}}^{2}}}{G\frac{{{M}_{e}}\times m}{{{R}_{e}}^{2}}}\]
Or, \[\frac{{{W}_{m}}}{{{W}_{e}}}=\frac{{{M}_{m}}}{{{M}_{e}}}\times \frac{{{R}_{e}}^{2}}{{{R}_{m}}^{2}}\]
We have \[{{M}_{e}}=6\times {{10}^{24}}kg\]
\[{{M}_{m}}=7.4\times {{10}^{22}}kg\]
\[{{R}_{e}}=6,400\,km\]
\[{{R}_{m}}=1,740\,km\]
Putting these data in the above equation we get,
\[\frac{{{W}_{m}}}{{{W}_{e}}}=\frac{7.4\times {{10}^{22}}\times 6400\times 6400}{6\times {{10}^{24}}\times 1740\times 1740}=\frac{1}{6}\]
Or, \[\frac{{{W}_{m}}}{{{W}_{e}}}=\frac{1}{6}\] Or, \[{{W}_{m}}=\frac{1}{6}\times {{W}_{e}}\]
Thus, weight of an object on the moon is one sixth of its weight on the earth.
A ball is dropped from a certain height of a tower. Find the speed of ball at the end of 2 second.
(a) 9.8 m/s
(b) 1.6 m/s
(c) 9.6 m/s
(d) 3 m/s
(e) None of these
Answer: (b)
A stone is dropped from the top of a building with a height of 1.6 meter. Find the speed of stone before touching the ground.
(a) 5.6 m/s
(b) 1.6 m/s
(c) 9.6 m/s
(d) 3 m/s
(e) None of these
Answer: (a)
A ball is thrown upward with the speed of 19.6 m/sec. Find the speed of ball after 3 second.
(a) -9.6 m/s
(b) 5.6 m/s
(c) -9.8 m/s
(d) 19.6 m/s
(e) None of these
Answer: (c)
A stone is thrown upward with a speed of 19.6 m/s. Find the maximum height reached by the stone.
(a) 29.6 m
(b) 15.6 m
(c) 39.2 m
(d) 19.6 m
(e) None of these
Answer: (d)
Find the weight of the body with a mass of 10 kg.
(a) 9.6 N
(b) 29.2 N
(c) 98 N
(d) 19.6 N
(e) None of these
Answer: (c)
You need to login to perform this action.
You will be redirected in
3 sec
