9th Class Science Gravitation and Floatation Earth?s Gravitational Force

        Earth’s Gravitation Force

Let us consider an object of mass 'm' and let 'M' be the mass of earth. The distance between the object and the centre of earth is approximately equal to the radius of the earth. Let R be the distance between object and the centre of earth. Then by universal law of Gravitation we have,

 \[F=G\,\,\frac{m\times M}{{{R}^{2}}}\]

Where, M = mass of earth \[=6\times {{10}^{24}}kg\]

R = radius of the earth \[=6.4\times {{10}^{6}}\] meters = 6,400 km

\[G=6.67\times {{10}^{-11}}\,N{{m}^{2}}/k{{g}^{2}}\]

The force between any object on the earth and the earth itself is very large, as compared to the force between any two object on the surface of earth, which is found to be negligible. The gravitational force exerted by the earth is called the force of gravity.

            Importance of Gravitational Force

The universal law of gravitation has many importance such as :

• It helps us to binds with the earth.
• The motion of moon around the earth is due to the gravitational force.
• It also helps the planets to revolve around the sun.
• Regular eruption of tides in the ocean and sea is due to gravitational force.

          Two objects of mass 200 kg and 800 kg separated by a distance of 50 m. Find the gravitational force between the two bodies.

(a) \[4.26\times {{10}^{-9}}N\]

(b) \[2\times {{10}^{-9}}N\]

(c) \[2.4\times {{10}^{-9}}N\]

(d) \[2.4\times {{10}^{-8}}N\]

(e) None of these

Answer: (a)

Explanation

We have, \[F=G\frac{mM}{{{r}^{2}}}\]

Or,  \[F=\frac{6.67\times {{10}^{-11}}\times 200\times 800}{50\times 50}=4.26\times {{10}^{-9}}N\]

       The mass of earth is \[6\times {{10}^{24}}kg\] and the mass of other planet is \[7.4\times {{10}^{22}}kg\]. If the distance between the earth and the other planet is \[3.84\times {{10}^{5}}km,\] find the force of attraction between the earth and the other planet.

(a) \[4.01\times {{10}^{20}}N\]

(b) \[3.31\times {{10}^{20}}N\]

(c) \[5.23\times {{10}^{20}}N\]

(d) \[2.01\times {{10}^{10}}N\]

(e) None of these

Answer: (a)

Explanation

We have \[F=G\frac{nM}{{{r}^{2}}}\]

Or, \[F=\frac{6.67\times {{10}^{-11}}\times 6\times {{10}^{24}}\times 7.4\times {{10}^{22}}}{(3.84\times {{10}^{5}})}=2.01\times {{10}^{20}}\,\] Newton

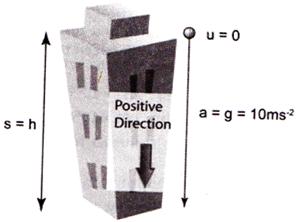
Bodies falling freely on the Earth

We know that the speed of a falling object increases as it comes down i.e. we can say that the object accelerates as it falls down. Suppose we drop a stone and a sheet of paper from a certain height, we find that the stone reaches the ground first and the sheet of paper later, which is quite expected. But we cannot generalized  this concept that heavier object falls faster than the lighter one.

For example: if we drop two different masses say 2 kg and 3 kg from same height we will find that they reaches the ground almost simultaneously. Thus, we can say that it is the density and the surface area of the object which determine the fall of object. The object having lesser density and lesser surface area such as, a sheet of paper, will have more air resistance which is not negligible. On the other hand the object having more density and lesser surface area such as stone or coin, the air resistance will be negligible Thus we can

conclude that if air is totally removed then stone and sheet of paper when dropped from a certain height, will reach the ground simultaneously