Gravitation
Category : 9th Class
Gravitation
Gravitation
When we throw .an object in upward direction it comes down automatically. This happens because of the force of gravitation. Actually the earth exerts a force of attraction that is called gravity on the object and pulls it down.

Isaac newton
The gravitational force was discovered by Sir Isaac Newton. One day he was sitting under an apple tree, suddenly an apple fell down from the tree. He started thinking about it. He concluded that the earth has certain force that attracted the apple. Finally he concluded that the earth attracts all the objects towards its centre and this force of attraction is called gravitational force of the earth or the gravity. The gravitational force of the earth is responsible for many phenomenons that take place around us. For example, the gravitational force is responsible for holding the atmosphere of the earth, falling of rain on the earth, flowing water in the rivers, walking, etc.
Every object in the universe attracts every other object with a certain force that is called gravitational force. The masses of the objects decide the amount of gravitational force a body can have. When we throw a stone in upward direction, it comes down after attaining a certain height. The earth pulls the stone towards its centre. The stone also pulls the earth toward it with the same force. As mass of earth is very large therefore the accleration produced becomes negligible. Due to this reason we do not see the earth moving towards the stone.
Universal Law of Gravitation
The great scientist Newton has given us the universal law of gravitation. According to this law, every object in the universe attracts every other object with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. The direction of the force is along the line joining the centres of two objects.
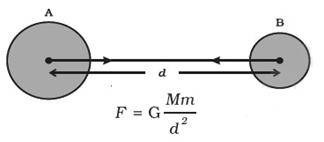
Gravitational force is directed along the line joining the centre of uniform objects
Let two objects P and Q of masses M and m lie at a distance d from each other, as shown in the above figure. Suppose the force of attraction between two objects is F. As per the universal law of gravitation, the force between the two objects is directly proportional to the product of their masses.
Therefore,\[F\propto M\times m\] —————— (1)
The force between two objects is inversely proportional to the square of the distance between them.
Therefore, \[F\propto \frac{1}{{{d}^{2.}}}\] ————— (2)
From equation (1) and (2) we get
\[F\propto \frac{M\times m}{{{d}^{2}}}.\]
Or, \[F=G\frac{M\times m}{{{d}^{2}}}\]—————(3)
Where G is constant of proportionality, it is called the universal gravitational constant.
The value of G is \[6.673\times {{10}^{-11}}N{{m}^{2}}/k{{g}^{2}}\]
The S.I. unit of G can be obtained by substituting the units of force, distance and mass in equation (3) as \[N\,{{m}^{2\,}}k{{g}^{-2}}.\]
Free Fall
When an object falls from a certain height towards the earth under the gravitational force of the earth and no other force acts on it, it is called free fall. As we have mentioned earlier the earth attracts objects towards it, so whenever an object falls towards the earth under the force of gravity we call it a free fall. During the free fall there is no change in the direction of motion of the objects, but due to the gravitational force of the earth there is a change in the magnitude of the velocity. Thus the falling objects have acceleration and this acceleration is called the acceleration due to gravity.
Acceleration Due to Gravity
When an object is dropped from some height, a uniform acceleration is produced in it by the gravitational pull of the earth that does not depends on the mass of the falling body. The uniform acceleration produced in the freely falling body due to the gravitational force of the earth is known as acceleration due to gravity. It is denoted by letter g. The value of g is taken as \[9.8\,\,m/{{s}^{2}}\]for most of the purposes.
Calculation of the Acceleration Due to Gravity
Let an object of mass m moving freely near the earth's surface. Neglecting air resistance, the only force on it is due to gravity. The force has magnitude
\[F=\frac{G{{M}_{e}}m}{R_{e}^{2}},\] ...(i)
Where \[{{\text{M}}_{\text{e}}}\,\text{=}\,\]mass of the earth, m = mass of the object, and \[{{\text{R}}_{\text{e}}}\,\text{=}\]radius of the earth.
As the earth's radius \[{{R}_{e}}(6,400\text{ }km)\] is large as compared to distance of the object from earth's surface, we use \[{{\text{R}}_{\text{e}}}\] in Equation (i) to denote the distance of the object from the centre of the earth. As the force given by Equation (i) is the resultant force on the object, its acceleration is
\[a=\frac{F}{m}=\frac{G{{M}_{e}}}{R_{e}^{2}}\]
Note that this acceleration does not depend on the mass of the object. Thus we have the following.
If gravity is the only (meaning that air resistance is neglected), all objects move with the same acceleration near the earth's surface. This acceleration is called the acceleration due to gravity, whose magnitude 'g' is given by
\[g\,=\,\frac{G{{M}_{e}}}{{{R}_{e}}^{2}}\]
\[=\,\frac{\left[ 6.67\times {{10}^{-11}}\,\frac{N{{m}^{2}}}{k{{g}^{2}}} \right]\times \left( 6\times {{10}^{24}}kg \right)}{{{\left( 6.4\times {{10}^{6}}m \right)}^{2}}}\,\approx \,9.8m/{{s}^{2}}.\]
The direction of this acceleration is towards the centre of the earth, i.e., in the vertically downward direction.
Equation of Motion for Freely Falling Bodies
To find the equation for the freely falling bodies that fall with uniform acceleration we need to slightly change the equations of motion. For freely falling bodies, the acceleration due to gravity is g. Therefore, replace a from g in the equations of motion. We get:
\[v=u+gt\]
\[h\,ut\,+\,\frac{1}{2}g{{t}^{2}}\]
\[{{v}^{2}}\,=\,{{u}^{2}}\,+\,2gh\]
Mass
The mass of an object is the quantity of material contained in it. It is always constant and does not change from place to place. Mass is a scalar quantity because it has only magnitude. The S.I. unit of mass is kilogram.
Weight
The weight of an object is the force with which it is attracted towards the earth. We
Know: \[F=m\times a\]
OR
\[F=m\times g\]
The force of attraction of the earth on an object is known as weight. Therefore, we can replace F with W Thus we get W = m x g. The S.I. unit if weight is Newton. Weight is a vector quantity as it has magnitude as well as direction. The weight of a body is not constant. It changes from place to place. For example, whatever be the weight of an object on the surface of the earth, its weight becomes zero when it is taken to the centre of the earth because g is zero at the centre of the earth. The weight of an object on the moon will be about \[1/{{6}^{th}}\] of what it is on the earth because the gravitational force of the moon is about \[1/{{6}^{th}}\] that of the earth.
The formula to derive the weight of an object on the moon is:
\[{{W}_{m}}\,=\,G\times \frac{M\times m}{{{R}^{2}}}\]
Thrust and Pressure
Here we are going to consider about the two examples of pushing a wood, first from a thumb and then from a drawing pin. When we push hard on a piece of wood with our thumb it doesn't go inside the wood, but if we repeat the same activity with a drawing pin into the wood with the same force the pin goes into the wood. The reason for the same is the force acting per unit area. In the first case that is pushing a wood from the thumb, the force is applied on the large area that's why it doesn't go into the wood whereas with a drawing pin the force is applied on a very small area and it goes into the wood. Thus we can say that the affect of a force depends on the area of the object on which it acts.
The same force can produce different pressures because it largely depends on the area over which it acts. Acting on a larger area produces small pressure whereas acting on a small area produces large pressure.
Thrust
The force acting on an object perpendicular to the surface is called thrust. The S.I unit of thrust is newton (N).
Pressure
The thrust per unit area is called pressure.
\[\text{Pressure=}\frac{\text{Thrust}}{\text{Area}}\]
The S.I. unit of pressure is \[N/{{m}^{2}}\] or \[N{{m}^{-2}},\] which is also called pascal (Pa). Thus
1 Pascal = 1 Newton per metre square
Or, \[1\,pa\,=\,1N/{{m}^{2}}\]
Pressure in Fluids
F'luids are the substances that can flow easily. All liquids and gases are fluids. A fluid can exert pressure in all directions. Pressure exerted by fluids increases with depth.
Buoyancy
When we place an object in a liquid, the liquid exerts an upward force on the object. For example, when we try to press a cork inside the water, it comes out on the surface. If we lift a. stone lying at the bottom of the pond, it appears very light when it is inside water, but it appears heavier when it is lifted into the air. The object appears to be light when is submerged in water and heavier when it is taken out of water. The reason for the some is every liquid exerts an upward force on the objects immersed in it. The tendency of a liquid to exert an upward force on an object placed in it is called buoyancy. If we immerse an object in a liquid it experiences an upward force called buoyant force. The upward force exerted by a liquid is also known as upthrust. It is the buoyant force which make the heavy objects lighter in water.
Factors that Affect Buoyant Force
The following are the factors that affect the buoyant force:
(i) Volume of object immersed in liquid: The volume of a solid object immersed inside the liquid increases the buoyant force and once the object is completely immersed in the liquid the buoyant force becomes the maximum. The magnitude of the buoyant force acting on a solid object does not depend on the nature of the solid object.
(ii) Density of the liquid: The liquid that has higher density exerts more upward buoyant force than the liquid having lower density. It is easier to swim in sea water because sea water has higher density and thus exerts a great buoyant force on the swimmer.
Archimedes' Principle
When a body is immersed fully or partially in a fluid, it experiences an upward force that is equal to the weight of the fluid displaced by it.
rce acting on an object = weight of liquid displaced by that object.
The following are the applications of Archimedes' Principle:
(i) It is used in designing ships and submarines.
(ii) It is used in lactometers, which are used to determine the purity of a sample of milk.
(iii) It is used in hydrometers used for determining density of liquids, are based on this principle.
(iv) It is used in determining the relative density of a substance.
Relative Density
The relative density of a substance is the ratio of its density to that of water.
Relative density of a substance\[\text{=}\frac{\text{Density}\,\text{of}\,\text{the}\,\text{substance}}{\text{Density}\,\text{of}\,\text{water}}\]
It means the relative density of a substance is the ratio of the mass of any volume of the substance to the mass of an equal volume of water. It expresses the heaviness of the substance in comparison to water.
Example:
Relative density of silver is 10.8. The density of water is\[{{10}^{3}}kg\,\,{{m}^{-3}}\]. What is the density of silver in SI unit?
Solution:
Relative density of silver = 10.8
Relative density \[\text{=}\,\frac{\text{Density}\,\text{of}\,\text{silver}}{\text{Density}\,\text{of}\ \text{water}}\]
Density of silver = Relative density of silver \[\times \] density of water
\[=\,10.8\times {{10}^{3}}kg\,{{m}^{-3}}.\]
\[=\,10800\,kg\,{{m}^{-3}}\].
You need to login to perform this action.
You will be redirected in
3 sec
