Universal Law of Gravitation
Category : 9th Class
According to universal law of gravitation, every two object in this universe attracts each other with a force, which is directly proportional to the product of their masses and inversely proportional to the square of distance between them.
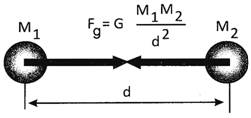
Let us consider two object of mass \[{{M}_{1}}\] and \[{{M}_{2}}\] and d be the distance between their centre. If F be the force between the two object, then
\[F\,\alpha {{M}_{1}}\times {{M}_{2}}\] and \[F\,\alpha \,\frac{1}{{{d}^{2}}}\]
Combining the above two equation we get,
\[F\,\alpha \,\frac{{{M}_{1}}\times {{M}_{2}}}{{{d}^{2}}}\]
Or, \[F=G\,\frac{{{M}_{1}}\times {{M}_{2}}}{{{d}^{2}}}\]
Where, G is universal gravitational constant.
The value of G is found to be \[\mathbf{6}\mathbf{.67\times 1}{{\mathbf{0}}^{\mathbf{-11}}}\mathbf{N}{{\mathbf{m}}^{\mathbf{2}}}\mathbf{/k}{{\mathbf{g}}^{\mathbf{2}}}\]. The value of G is called universal constant i.e. it remains same everywhere in this universe. It does not depend on anything. It is applicable for all particle whether small or large.
You need to login to perform this action.
You will be redirected in
3 sec
