Acceleration
Category : 9th Class
Acceleration
When a bus starts from a stand its velocity increases for some time. When it was at the stand the velocity was zero and after some time it's velocity gradually starts increasing and reaches maximum after some time. Again when it approaches the second stand its velocity gradually decreases and become zero. This means that the velocity of the bus changes during the motion. The rate at which the velocity of the object changes with the time is called the acceleration. Or we can say that velocity per unit time is called the acceleration. It is denoted by 'a'. It is given by,
Acceleration \[=\frac{\text{Change in Velocity}}{\text{Time}}\]
The SI unit of acceleration is metre/sec2 or m/s2
Let us consider the motion of the object along the straight line in the same direction. If 'U' be the initial velocity and 'V be the final velocity, then change in velocity in the time 't' is given by,
\[a=\frac{V-U}{t}\] or \[V=U+at\]
Observations
So, it is clear from the above example that acceleration need not always remain the same. It means that the speed of a moving body may increase, it can also decrease or may remain the same or become zero. In general, when the velocity of a body is changing, the body is said to be accelerating. Suppose a car starts from rest (initial velocity is zero) and its velocity increases at a steady rate so that after 5 seconds its velocity is 10 meters per second. Now, in 5 seconds the velocity has increased by 10 - 0 = 10 meter per second and in 1 second the velocity increases by \[\frac{10}{5}=2\] meter per second.
Uniform Acceleration
Consider a particle moving along a straight line in such a way that its velocity changes in equal amount, in equal time interval. If this happens, then the body is said to be moving with the uniform acceleration.
Velocity Time Graph for Uniform Acceleration
Velocity time graph for uniform acceleration is as shown below. For example, when a ball is dropped from a certain height its velocity continuously increases and uniformly. The graph below represents the motion.
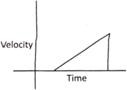
Thus area under the velocity time graph given the displacement of the object.
Area \[=\frac{1}{2}\times \,base\,\times height\]
The slope of the velocity time graph gives the acceleration of the object moving along the straight line.
Non- Uniform Acceleration
The object is said to have the non uniform acceleration, if the acceleration of the object moving along a straight line is not constant.
If the speed of an object decreases, its acceleration is negative. It is known as retardation. Since acceleration is a vector quantity, it has a direction associated with it.
The direction of the acceleration vector depends on two things:
For a free falling body, acceleration is in vertically downward direction.
If an object is slowing down, then its acceleration is in the opposite direction of its motion.
| Example A | |
| Time (s) | Velocity (m/s) |
| 0 | 0 |
| 1 | 4 |
| 2 | 8 |
| 3 | 16 |
| 4 | 32 |
| Example C | |
| Time (s) | Velocity (m/s) |
| 0 | 32 |
| 1 | 16 |
| 2 | 8 |
| 3 | 4 |
| 4 | 0 |
| Example B | |
| Time (s) | Velocity (m/s) |
| 0 | -8 |
| 1 | -6 |
| 2 | -4 |
| 3 | -2 |
| 4 | -0 |
| Example D | |
| Time (s) | Velocity (m/s) |
| 0 | 0 |
| 1 | -2 |
| 2 | -4 |
| 3 | -6 |
| 4 | -8 |
These are both examples of negative acceleration
If the velocity of a body increases along a straight line, the acceleration is positive, and if the velocity of a body decreases, the acceleration is negative.
Retardation \[=\frac{\text{change in velocity}}{\text{time taken}}\] and has the same unit as that of acceleration (m/s2)
Types of Acceleration
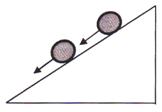
Positive acceleration: When a ball rolls down on an inclined plane the velocity of the ball increases and it is said to be moving with positive acceleration.
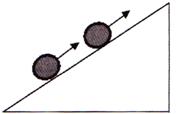
Negative acceleration : When a ball rolls up on an inclined plane the velocity of the ball decreases and it said to be moving with negative acceleration or retardation or declaration.
A ball thrown vertically upwards is also an example of negative acceleration.
Non-uniform acceleration: A car moving on a crowded road. It has to change its speed every now and then due to the traffic on the road.
Find the acceleration of the bus whose speed changes from 35 m/s to 20 m/s in 5 seconds.
(a) \[+\,3\,m/{{s}^{2}}\]
(b) \[-3\,m/{{s}^{2}}\]
(c) \[15\,m/{{s}^{2}}\]
(d) \[-25\,m/{{s}^{2}}\]
(e) None of these
Answer: (b)
Explanation
(b) Initial velocity of car, \[u=35\,m/s\]
Final velocity of car, \[v=20\,m/s\]
And, time taken, \[t=5\,s\]
Now, putting these values in the formula for acceleration :
\[a=\frac{V-U}{t}\]
We get, \[a=\frac{20-35}{5}\,m/{{s}^{2}}=\frac{-15}{5}\,=-3m/{{s}^{2}}\]
The negative sign of acceleration means that it is retardation. So, we can also say that the car has a retardation of \[-3\,m/{{s}^{2}}\].
Which of the quantity distance, speed, velocity or acceleration decides the direction of motion of the body?
(a) Speed
(b) Velocity
(c) Acceleration
(d) Distance
(e) None of these
Answer: (b)
Explanation
It is the velocity, which decides the direction of motion of the body. The accelerartion simply tells the rate of change of velocity. When a body is thrown upwards, its direction of velocity is upwards, that is why the body goes upward, whereas its acceleration is downwards.
Graphical Representation of Motion
Distance Time Graphs
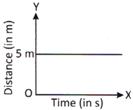
Distance - time graph for a stationary body is straight line parallel to time - axis. From graph, at t = 0, body is at 5 m from reference point. It will remain at 5 m for all times.
(a) If position - time graph is a straight line it indicates uniform or constant velocity. velocity = slope of straight line e.g. slope \[=\frac{AB}{OB}\]
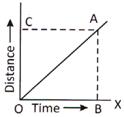
For non - uniform motion, position time graph is not a straight line, it is a curve line. Slope of the graph is different at different point
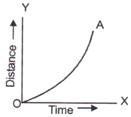
Velocity of the increases as slope is increasing
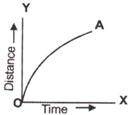
Velocity of body decreases as slope is decreasing
Velocity time graph
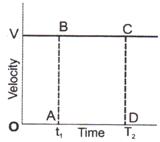
If the Velocity-time graph of a body is a straight line parallel to the time axis, then the speed of the body remains constant (or uniform).
Distance covered = Area under graph
From graph, distance covered in time interval \[{{t}_{1}}\] to \[{{t}_{2}}\]
S = area ABCD = v \[({{t}_{2}}-{{t}_{1}})\]
(a) If velocity time graph is a straight line, it indicates uniform acceleration
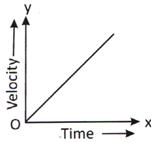
(b) Slope = Acceleration
(c) Area under graph = distance or displacement
Velocity-time Graph when the initial velocity of the body is not zero from graph, initially at t = 0, velocity = 2ms-1.
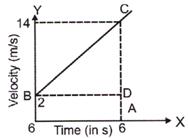
Acceleration = slope \[=\frac{CD}{BD}=\frac{14-2}{6}\]
\[=2\,m/s\]
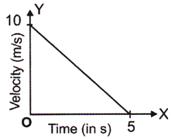
Acceleration = slope \[=\frac{0-10}{5-0}\]
\[=-2\,\,m/{{s}^{2}}\]
Negative acceleration indicates retardation
Velocity- time graph of non uniform velocity
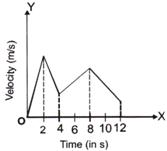
From the graph, velocity of the body is increasing at constant rate upto 2 s, and then the velocity is decreasing at a constant rate upto 4 s. Again velocity is increasing upto 8 s and then decreasing upto to 12 s.
Figure shows distance - time graphs of two objects A and B. Which object is moving with a greater speed when both are moving?
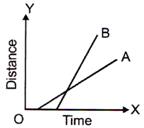
(a) A is taster than B
(b) B is faster than A
(c) Both A and B have same speed
(d) All of these
(e) None of these
Answer: (b)
Expiations
The line for object B makes a larger angle with the time-axis. Its slope is, therefore, larger than the slope of the line for obejct A.
Thus, the speed of B is greater than that of A.
What is the distance covered by a particle during the time interval t = 0 to t = 20 for which the speed - time graph is shown in Figure.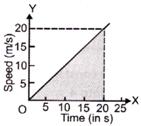 
(a) 400m
(b) 100 m
(c) 200m
(d) All of these
(e) None of these
Answer: (c)
Explanation
The distance covered in the time interval 0 to 20 s = area of the triangle. Distance \[=\frac{1}{2}\times \] base x height \[=\frac{1}{2}\times \,(20\,s)\times \,(20\,m/s)\,=200\,m\]
You need to login to perform this action.
You will be redirected in
3 sec
