Distance and Displacement
Category : 9th Class
| S. No. | Distance | S. No. | Displacement |
| 1. | Distance is the length of the actual path traveled by an object in a given interval of time. | 1. | Displacement is the shortest distance between the initial and final positions of a moving object in a particular direction. |
| 2. | Distance traveled by an object depends upon the path followed by the particle in going from initial position to the final position. | 2. | The displacement of an object between initial and final positions of the particle does not depend upon the path followed by it. |
| 3. | Distance traveled by an object in a given interval of time is always positive. | 3. | Displacement of an object in a given interval of time may be positive, negative or zero. |
| 4. | Distance is a scalar quantity. | 4. | Displacement is a vector quantity. |
Now let us consider an object changing its position, with respect to a fixed point called the origin 0. \[{{x}_{i}}\] and \[{{x}_{f}}\] are the initial position and final position of the object. Then the displacement of the object \[={{x}_{f}}-{{x}_{i}}\].
Case 1: Suppose the object is moving from + 1 to + 6 then displacement \[-{{x}_{i}}\]
\[=+6-\,(+1)=+5\]

Case 2: If the object is moving from -2 to 3 then displacement \[={{x}_{f}}-{{x}_{i}}\]
\[=3-\,(-2)=+\,5\]

Case 3: if the object is moving from +6 to -1 then displacement \[={{x}_{f}}-xi\]
\[=+1\,-(+\,6)=-5\]

Case 4: if the follows the path as shown in the figure then the final position and the initial position is the same i.e., the displacement is zero
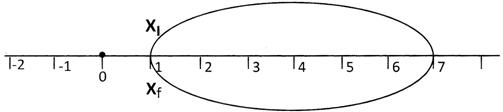
From the above examples, we can conclude that the displacement of a body is positive if its position lies on the right side of the initial position and negative if its final position is on the left side of its initial position. Whenever a moving object comes back to the original position then the displacement is zero.

![]() If a body moves 6 m towards south and then turns towards east and moves 8 m, then find the displacement of the body from the initial position?
If a body moves 6 m towards south and then turns towards east and moves 8 m, then find the displacement of the body from the initial position?
(a) 12 m
(b) 8 m
(c) 10 m
(d) 6 m
(e) None of these
Answer: (c)
![]() A man travels a distance of 2 m towards East, then 6 m towards South and finally 6 m towards East. Find the resultant displacement.
A man travels a distance of 2 m towards East, then 6 m towards South and finally 6 m towards East. Find the resultant displacement.
(a) 6 m
(b) 9 m
(c) 11 m
(d) 10 m
(e) None of these
Answer: (d)
![]() Speed
Speed
It is defined as the distance traveled by the body per unit time. If the distance of the body is 'S' in time T, then its speed 'M' is given by:
\[V=\frac{s}{t}\]
Where V = Speed,
S = Distance,
and t = time taken (to travel that distance )
SI unit of Speed is m/s or \[m{{s}^{-1}}\].
The small values of Speed are expressed in the units of centimeter per second which is written as cm/s or \[cm\,{{s}^{-1}}\].
To express high speed values, we use the unit of kilometer per hour, written as km. p.h. or km/h or \[km\,{{h}^{-1}}\]. Speed is a scalar quantity, as it has only magnitude, no specific direction.
![]()
In a race different participants start running at the same time and cover the same distance in different time intervals. The participant who takes the minimum time to cover the distance is considered as the winner. Suppose Sidhant and Dhanajay take 15 minutes and 10 minutes respectively to cover a distance of 1000 m, who is faster? To find out who is faster we have to calculate the distance covered by Sidhant and Dhanajay in one minute i.e., Sidhant covers more distance in unit time or in other words we can conclude that Sidhant covered the distance with greater speed. Speed can be defined as the distance covered by a moving object in unit time. The speed of a body gives us an idea of how slow or fast that body is moving. Speed of a body is the distance traveled by it per unit time.
\[\text{Speed}\,=\,\frac{\text{Distance travelled}}{\text{time taken}}\]
![]() Uniform Speed
Uniform Speed
Below figure represents the distance covered by the object per second between two fixed points X and Y.

The object covers 10 meters in every one second, hence the speed of the object is 10 m/s between the points X and Y. Thus we see that the speed of object remains the same between any two points in between the given fixed points.
Hence we can say that the object is moving with the uniform speed. An object is said to be moving with uniform speed if it covers equal distances in equal interval of time.
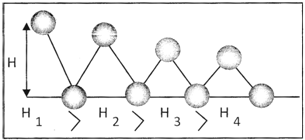
![]() Non-Uniform Speed
Non-Uniform Speed
The above example holds good only if friction or resistance offered by the surface is ignored. The distance covered varies with time.
![]()
A bouncing ball bounces off to a height less than the initial height and slowly the height decreases. The distance covered by the ball decreases with time. That means the speed of the ball varies from point to point. This type of speed is called a variable speed.
An object is said to be moving with variable speed or non-uniform speed if it covers equal distances in unequal intervals of time or vice-versa.
Average Speed and Instantaneous Speed
When we move on the road in our vehicle, we find that we have to change the speed of the vehicle several times before we reach our destination. Thus, we can say that our speed does not remain the same throughout the journey. In such case we calculate the speed of the journey by taking the ratio of the total distance traveled, by the total time taken to cover the distance.
Average Speed \[=\,\frac{\text{Total Distance}}{\text{Total Time}}\]
If a car covers a distance \[{{s}_{1}}\] in time \[{{t}_{1}},\] distance \[{{s}_{2}}\] in time \[{{t}_{2}}\] and distances \[{{s}_{n}}\] in time \[{{t}_{n}}\] then the average speed is given by,
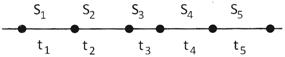
The average speed of a body is the total distance covered by the body divided by the total time taken to cover that distance.
Average speed \[=\,\frac{\text{Total Distance}}{\text{Total Time}}\] \[=\,\frac{({{s}_{1}}+{{s}_{2}}+{{s}_{3}}+{{s}_{4}}+{{s}_{5}})}{({{t}_{1}}+{{t}_{2}}+{{t}_{3}}+{{t}_{4}}+{{t}_{5}})}\]
![]() Instantaneous Speed
Instantaneous Speed
You must have observed two meters in the vehicles one is 'speedometer' and another one is 'odometer'. The speedometer gives the speed in kilometer per hour and the 'odometer' records the distance traveled in kilometers. If the 'speedometer' shows 80 km/h, it doesn't mean that the vehicle is moving with the speed of 80km/h throughout the journey. The actual speed of the vehicle may be less than or greater than that. The 'speedometer' shows the speed at a particular instant of time, and is known as instantaneous speed..
You need to login to perform this action.
You will be redirected in
3 sec
