Data Representation and Number System
Category : Banking
Data Representation and Number System
Introduction
Data representation is a method to represent data in a computer. In computer we enter different forms of data such as number, text, graphics, sound etc. All These data look different, but in the computer process all are in only one form, that is, 0 and 1, binary or digital form. Each information is stored in a computer as a digital data. Generally, we use the decimal number system which, with the help of 0 to 9, represents any number. But in a computer any number is represented by a combination of 0 and 1. These are the number systems used in computer
1. Binary Number System
2. Octal Number System
3. Hexadecimal Number System
Binary Number system: In the binary number system, there are only two possible values 0 and 1 which represent the ON and OFF state of electrical pulse in the circuit. These 0 and 1 are binary digits and each is called a bit. This number system is used by computer to data process and storage.
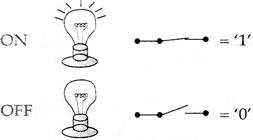
In decimal number system there is a base of 10, because there are 10 has a place and that is called place value. Such as in a decimal number 17, place value of 1 is 10 and 7 is 1. But in a binary number system there is a base of 2 because there are 2 possible digits (0 and 1). Each digit position in a binary number represents a power of two. So, when we write a binary number, each binary digit is multiplied by an appropriate power.
Conversion of Decimal to Binary: To convert decimal to binary we simply divide the decimal value by 2 and then write down the remainder, we rapid this press until we cannot divide it by 2 anymore
Example
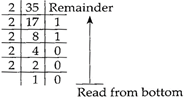
\[\therefore \text{ (35}{{\text{)}}_{10}}={{(100011)}_{2}}\]
Conversion of Binary to Decimal: To convert binary to decimal we simply multiply the digits of binary value by its place value and then add all the values we get from multiplication.
Example: Convert \[{{(100011)}_{2}}\]to its decimal equivalent
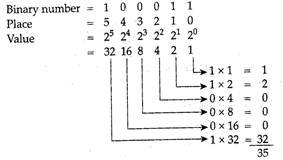
\[100011=1*{{2}^{5}}+0*{{2}^{4}}+0*{{2}^{2}}+1*{{2}^{1}}+1*{{2}^{0}}\]
\[\therefore {{(100011)}_{2}}={{(35)}_{10}}\]
1. Octal Number system: system there is base of 8 because there is 8 possible digit (0and7) each digit position in an octal number represent in a power Number represents a power of eight. Each octal digit is thus equivalent to three binary digits
|
Octal Number |
Equipment three binary digits |
|
0 |
000 |
|
1 |
001 |
|
2 |
010 |
|
3 |
011 |
|
4 |
100 |
|
5 |
101 |
|
6 |
110 |
|
7 |
111 |
Conversion of Decimal to Octal: To convert decimal to octal we simply divide the decimal value by 8 and then write down remember the decimal value by 8 and then write down the remainder. We repeat this process until we cannot divide by 8 anymore.
Example: Convert\[{{(385)}_{10}}\] to its binary equivalent.
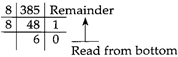
\[\therefore \] \[{{(385)}_{10}}={{(601)}_{8}}\]
Conversion of Octal to Decimal: To convert octal to decimal we simply multiply the digits of octal value by its place value and then add the value we get from multiplication.
Example: Convert \[{{(601)}_{8}}\] to its decimal equivalent.
\[{{(601)}_{8}}=6*{{8}^{2}}+0*{{8}^{1}}+1*{{8}^{0}}=384+0+1={{(385)}_{10}}\]
\[\therefore \]\[{{(601)}_{8}}={{(385)}_{10}}\]
Conversion of Octal to Binary
There are two methods to convert octal to binary.
1. To convert octal to binary we simplify multiply the digits of octal value by its place value and then add the value we get from multiplication. That is decimal value of octal number. Again we calculate the binary value of this decimal value.
Example: Convert \[{{(601)}_{8}}\] to its binary equivalent.
\[{{(601)}_{8}}=6*{{8}^{2}}+0*{{8}^{1}}+1*{{8}^{0}}=384+0+1={{(385)}_{10}}\]
\[\therefore \]\[{{(601)}_{8}}={{(385)}_{10}}\]
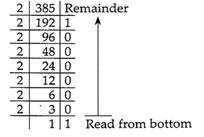
\[\therefore \] \[{{(601)}_{8}}={{(110000001)}_{2}}\]
2. Octal number Representative by collection of three digits of binary number such as octal number 1 is representative 001 in binary number system.
So to convert octal to binary we replace each digit of octal by three digit collection of the binary Number.
Example: Convert \[{{601}_{8}}\] to its binary equivalent.
\[{{601}_{8}}=110\,\,000\,\,001={{110000001}_{2}}\]
Conversion of Binary to Octal
There are two methods to convert octal to binary.
1. To convert binary to octal we simplify multiply the digits of octal value by its place value and then add the value we get from multiplication. That is decimal value of binary number. Again we calculate the octal value of this decimal value.
Example: Convert \[{{111010101}_{2}}\]to its octal equivalent.
\[{{111010101}_{2}}\]\[=1*{{2}^{8}}+1*{{2}^{7}}+1*{{2}^{6}}+0*{{2}^{5}}+\]\[1*{{2}^{4}}+0*{{2}^{3}}+1*{{2}^{2}}+0*{{2}^{1}}+1*{{2}^{0}}\]
\[=256+128+64+16+4+1={{469}_{10}}\]
\[\therefore \] \[{{111010101}_{2}}={{469}_{10}}\]
Again, we calculate the octal value of \[{{(469)}_{10}}\]
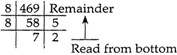
\[\therefore \] \[{{111010101}_{2}}={{725}_{8}}\]
To convert binary to octal we replace the three digits group of binary by its octal value.
Example: Convert \[{{111010101}_{2}}\] to its octal equivalent.
\[{{111010101}_{2}}=111\,\,010\,\,101={{725}_{8}}\]
Hexadecimal Number system: In Hexadecimal number system there is a base of 16 because there are16 possible digits (0 and 15). Each digit Position in a hexadecimal number represents a power of sixteen. In the Hexadecimal number system the numbers 0-9 are represented in their normal way, but numbers 10-15 are represented by the letters A-F respectively. Each hexadecimal digit is, thus, equivalent to four binary digits.
|
Hexadecimal |
Decimal |
Equivalent four binary digits |
|
0 |
0 |
0000 |
|
1 |
1 |
0001 |
|
2 |
2 |
0010 |
|
3 |
3 |
0011 |
|
4 |
4 |
0100 |
|
5 |
5 |
0101 |
|
6 |
6 |
0110 |
|
7 |
7 |
0111 |
|
8 |
8 |
1000 |
|
9 |
9 |
1001 |
|
A |
10 |
1010 |
|
B |
11 |
1011 |
|
C |
12 |
1100 |
|
D |
13 |
1101 |
|
E |
14 |
1110 |
|
F |
15 |
1111 |
Conversion of Decimal to Hexadecimal: To convert decimal to hexadecimal we simply divide the decimal value by 16 and then write down the remainder repeat this process until we cannot divide it by 16 anymore.
Example: Convert \[{{382}_{10}}\] to its hexadecimal equivalent Read from bottom
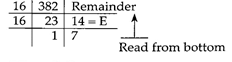
\[\therefore \] \[{{382}_{10}}=17{{E}_{16}}\]
Conversion of Hexadecimal to Decimal: To convert hexadecimal to decimal we simply multiply the digits of hexadecimal value by its place value and then add the value we get from multiplication. That is decimal value of Hexadecimal number again we calculate they binary value of this decimal value
Example: Convert \[{{10}_{6}}\]to its decimal equivalent.
\[{{10}_{6}}=1*{{16}^{1}}+0*{{16}^{0}}\]
\[\therefore \] \[{{10}_{16}}={{16}_{10}}\]
Conversion of Hexadecimal to Binary
There are to Method to convert octal two binary hexadecimal value by its place value and then add the value we get from multiplication. That is decimal value of hexadecimal number. Again we calculate the binary value of this decimal value.
Example: Convert \[B6{{A}_{16}}\]to its binary equivalent.
\[B6{{A}_{16}}=B*{{16}^{2}}+6*{{16}^{1}}+A*{{16}^{0}}\]
\[=11*256+6*16+10*1\]
\[=2816+96+10\]
\[={{2922}_{10}}\]
\[\therefore \] \[B6{{A}_{16}}={{2922}_{10}}\]
Again, we calculate the binary value of 2922,p
\[~B6{{A}_{16}}=B*{{16}^{2}}+6*{{16}^{1}}+A*{{16}^{0}}\]
\[=11*256+6*16+10*1\]
\[=2816+96+10\]
\[{{2922}_{10}}\]
\[B6{{A}_{16}}={{2922}_{10}}\]

\[\therefore \] \[B6{{A}_{16}}={{101101101010}_{2}}\]
2. Hexadecimal number is represented by a collection of four digits of binary number, such as hexadecimal number 1 is represented by 0001 in binary number system of hexadecimal by four digit collection of binary number.
So to convert hexadecimal to binary we replace each digit of hexadecimal by four digit collection of binary number.
Example: Convert \[B6{{A}_{16}}\] to its binary equivalent.\[B6{{A}_{16}}=1011\,\,0110\,\,1010={{101101101010}_{2}}\]
Conversion of Binary to Hexadecimal
To convert binary to hexadecimal we replace the four digits group of Binary by its hexadecimal value.
Example: Convert \[{{101101111}_{2}}\] to its hexadecimal equivalent.
\[{{101101111}_{2}}=0001\,\,0110\,\,{{1111}_{2}}=16{{F}_{16}}\]
Place value of digits
|
Number system |
Place Value |
|
Place value after decimal |
|||||
|
|
Thousand |
Hundred |
Tens |
Ones |
|
?1 |
?2 |
?3 |
|
Decimal |
\[{{10}^{3}}=1000\] |
\[{{10}^{2}}=100\] |
\[{{10}^{1}}=10\] |
\[{{10}^{0}}=1\] |
. |
\[{{10}^{-1}}\] |
\[{{10}^{-2}}\] |
\[{{10}^{-3}}\] |
|
|
|
|
|
|
|
\[=\frac{1}{10}\] |
\[=\frac{1}{100}\] |
\[=\frac{1}{1000}\] |
|
Binary |
\[{{2}^{3}}=8\] |
\[{{2}^{2}}=4\] |
\[{{2}^{1}}=2\] |
\[{{2}^{0}}=1\] |
. |
\[{{2}^{-1}}\] |
\[{{2}^{-2}}\] |
\[{{2}^{-3}}\] |
|
|
|
|
|
|
|
\[=\frac{1}{2}\] |
\[=\frac{1}{4}\] |
\[=\frac{1}{8}\] |
|
Octal |
\[{{8}^{3}}=512\] |
\[{{8}^{2}}=64\] |
\[{{8}^{1}}=8\] |
\[{{8}^{0}}=1\] |
. |
\[{{8}^{-1}}\] |
\[{{8}^{-2}}\] |
\[{{8}^{-3}}\] |
|
|
|
|
|
|
|
\[=\frac{1}{8}\] |
\[=\frac{1}{64}\] |
\[=\frac{1}{512}\] |
|
Hexadecimal |
\[{{16}^{3}}=4096\] |
\[{{16}^{2}}=256\] |
\[{{16}^{1}}=16\] |
\[{{16}^{0}}=1\] |
. |
\[{{16}^{-1}}\] |
\[{{16}^{-2}}\] |
\[{{16}^{-3}}\] |
|
|
|
|
|
|
|
\[=\frac{1}{16}\] |
\[=\frac{1}{256}\] |
\[=\frac{1}{4096}\] |
Adding Binary Numbers
Adding binary numbers is very similar to adding decimal numbers, but it uses only two digits 0 and 1.
There are four basic rules of binary addition
(i) 0+0=0
(ii) 0+1=1
(iii) 1+0=1
(iv) 1+1=0 (carry one because 1 + 1 = 10)
Example: Add\[{{1011011}_{2}}+{{100111}_{2}}\]
\[\begin{align}
& \underline{\begin{align}
& 1011011 \\
& +100111 \\
\end{align}} \\
& Carries-111111 \\
\end{align}\]
So.\[{{1011011}_{2}}+{{100111}_{2}}+{{10000010}_{2}}\]
Subtracting binary numbers
Subtracting binary numbers is very similar to subtracting decimal umbers, but it also uses only two digits 0 and 1. There are four basic rules of binary subtraction
(i) 0 ? 0 = 0
(ii) 0 ? 1 = 1 (borrow from nearest left side digit)
(iii) 1 ? 0 = 1
(iv) 1 ? 1 = 0
Example: Subtract\[{{1011011}_{2}}-{{100111}_{2}}\]
\[\begin{align}
& \underline{\begin{align}
& 1011011 \\
& -100111 \\
\end{align}} \\
& 110100 \\
\end{align}\]
So, \[{{1011011}_{2}}-{{100111}_{2}}={{110100}_{2}}\]
Binary Memory
Memory is a data storage device in a computer system. The data is stored in binary form (0 and 1).
Bit: A bit is the smallest unit of computer memory. There is only one value of a bit either 1 or 0.
Nibble: It is a sequence of four bits.
Byte: It is a sequence of 8 bits and any data can measure in a byte. To store in memory any alphabet, symbol or space etc. needs minimum one byte space.
Word: A word is a string of bits stored in computer memory. Word length can vary in different machines.
Memory measurement: Memory or any storage device's capacity is expressed as a quantity of bits or bytes, such as kilobyte, megabytes and Gigabyte etc. The total amount of stored information that a storage device or medium can hold is called a capacity of that memory or storage device.
|
4 bits |
1 Nibble |
|
1 Nibble |
1 byte |
|
8 bits |
1 kilobyte (KB) |
|
1024 bytes |
1 Megabyte (MB) |
|
1024 kilobytes |
1 Gigabyte (GB) |
|
1024 Gigabytes |
1 terabyte (TB) |
A gigabyte, is equal to approximately one billion bytes or a thousand megabytes. A gigabyte is equal to exactly 1,073,741,824 bytes and to 1,024 megabytes. A megabyte, is equal to about one million bytes, or exactly 1,048,576 bytes.
Computer Codes
In computer any characters like the alphabet, digit or any special character is represented by collection '1's and '0's in a unique coded pattern. These patterns are of different types, and are called computer codes.
There are three types of coding system-
1. Binary Coded Decimal (BCD): It is also called Packet decimal. Binary Coded Decimal is a number system where four bits are used to represent each decimal digit.
BCD Table
|
Decimal |
BCD |
Decimal |
BCD |
|
0 |
0000 |
5 |
0101 |
|
1 |
0001 |
6 |
0110 |
|
2 |
0010 |
7 |
0111 |
|
3 |
0011 |
8 |
1000 |
|
4 |
0100 |
9 |
1001 |
1. ASCII Code: It stands for American Standard Code for Information Interchange. In ASCII system a character is represented by seven bits.
2. EBCDIC Code: It stands for Extended Binary Coded Decimal Interchange code. In EBCDIC system a character is represented by eight bits. ASCII and EBCDIC are very popular coding systems.
Logic Gate: There are three basic gates in any digital system. They are AND, OR and NOT gate. Gate is an electronic circuit in which we can get Output by one or more but input.
And gate: This is the circuit of AND gate.
![]()
|
Switch A |
Switch B |
Switch C |
|
Off (0) |
Off (0) |
Off (0) |
|
Off (0) |
Off (1) |
Off (0) |
|
Off (1) |
Off (0) |
Off (0) |
|
Off (1) |
Off (1) |
Off (1) |
Means, \[C=A*B\]
OR gate: This is circuit of OR gate.
![]()
|
Switch A |
Switch B |
Switch C |
|
Off (0) |
Off (0) |
Off (0) |
|
Off (0) |
Off (1) |
Off (1) |
|
Off (1) |
Off (0) |
Off (1) |
|
Off (1) |
Off (1) |
Off (1) |
Means,\[C=A+B\]
NOT gate: This is circuit of NOT gate.
![]()
|
Switch A |
Switch B |
|
Off (0) |
ON (1) |
|
ON (11) |
Of (0) |
Means, \[B=\overline{A}\]
All other gates can be constructed by using these three gates.
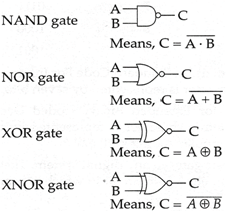
NAND gate and NOR gate are called Universal gates because by using these gates any digital circuit can be constructed.
You need to login to perform this action.
You will be redirected in
3 sec
