Heat
Category : Banking
Introduction
Temperature is defined as the degree of hotness or coldness of a body. It is a scalar quantity Its S.I. unit is kelvin (K). Heat is a form of energy -which causes sensation of hotness or coldness. The flow of heat is always from higher temperature to lower temperature. No heat flows from one body to other, when both the bodies are at the same temperature. The two bodies are said to be in thermal equilibrium. The SI unit of heat is joule. Its CGS unit is calorie, 1 cal = 4.2 joule
A branch of science which deals with the measurement of temperature of a substance is called thermometry. Thermometer is a device used to measure the temperature. Thermometer used for measuring very high temperatures are called pyrometer.
\[\frac{C-0}{100}=\frac{F-32}{212-32}=\frac{K-273.16}{373.16-273.16}\]=\[\frac{R-0}{80-0}=\frac{Ra-460}{672-460}\]\[{{T}^{0}}(K)=({{t}^{0}}C+273.16)\] Normal temperature of human body is 310.15 K\[({{37}^{0}}C={{98.6}^{0}}F)\] STP or NTP implies 273.15 K \[({{0}^{0}}C={{32}^{0}}F)\]
The equation, PV= nRT where, n = number of moles in the sample of gas R = universal gas constant; (its value is 8.31\[J\,mo{{l}^{-1}}{{K}^{-1}}\]), is known as ideal-gas equation. It is the combination of following three laws
(i) Boyle's law: When temperature is held constant, the pressure is inversely proportional to volume. i.e., \[P\propto \frac{1}{V}\](at constant temperature)
(ii) Charters law: When the pressure is held constant, the volume of the gas is directly porportional to the absolute temperature. i.e., \[V\propto T\](at constant pressure)
(iii) Avogadro's law: When the pressure and temperature are kept constant, the volume is directly proportional to the number of moles of the ideal gas in the container. i.e., \[V\propto n\](at constant pressure and temperature)
The lowest temperature of\[-\,273.16{}^\circ C\] at which a gas is supposed to have zero volume and zero pressure and at which entire molecular motion stops is called absolute zero temperature. A new scale of temperature starting with \[-273.16{}^\circ C\]by Lord Kelvin as zero. This is called Kelvin scale or absolute scale of temperature. \[T\left( K \right)=t{}^\circ C+273.16\]
Thermal Expansion
The increase in the dimensions of a body due to the increase in its temperature is called thermal expansion.
Almost all liquids expand on heating but water when heated from \[0{}^\circ C\] to \[4{}^\circ C\] its volume decreases and hence density increases until its temperature reaches\[4{}^\circ C\]. Its density is maximum at\[4{}^\circ C\]on farther heating its density decreases. This behaviour of water is called anomalous behaviour of water.
Specific Heat Capacity
It is the amount of heat energy needed to raise the temperature of unit mass of substance by \[1{}^\circ C\](or 1K). It is denoted by s or c. \[c=\frac{1}{m}\frac{dQ}{dT}\]
When state of a substance changes, change of state takes place at constant temperature (m.pt or b.pt.) heat is released or absorbed and is given by, Q=mL where L is latent heat The SI unit of latent heat is J/kg
Change of State
Any state of a substance (solid/ liquid/ gas) can be changed into another by heating or cooling. The transition of a substance from one state to another is called a change of state.
(i) Melting: When heat is supplied, solid substance changes into liquid, this change of state of substance is called melting. \[Solid\xrightarrow{Heat}Liquid\] The temperature at which the solid and the liquid states of a substance coexist in thermal equilibrium with each other is called its melting point.
(ii) Freezing: When heat is released, liquid changes into solid, this change of state of substance is called freezing.
\[Liquid\xrightarrow{cool}solid\]
(iii) Condensation: When vapour is cooled, it changes into liquid, this change of state is called condensation
\[Vapour\xrightarrow{cool}liquid\]
(iv) Evaporation: Conversion of liquid into gaseous state at all the temperatures is called evaporation or boiling.
\[Liquid\xrightarrow{Heat}Vapour\] The temperature at which the liquid and vapour states of a substance consist in thermal equilibrium with each other is called its boiling point. It is a phenomenon that occurs at the surface of liquids. The rate of calibration increases with rise in temperature. Heat required to change unit mass of liquid into vapour at a given temperature is called heat of evaporation at that temperature.
(v) Sublimation: It is the conversion of a solid directly into vapours. \[Solid\xrightarrow{Heat}Vapour\] Sublimation takes place when boiling point is less than the melting point.
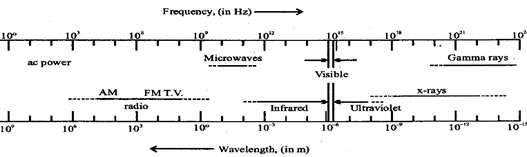
(i) A perfectly black body absorbs all the radiant heat incident upon it. (i.e. a=1)
(ii) A perfectly black body does not reflect or transmit the radiant heat incident upon it. (i.e. t = 0, r = 0)
(iii) The coefficient of emission of a perfectly black body is 1. It is very good emitter of heat.
According to Wien's displacement law
\[{{\lambda }_{m}}\times T=b\]
Here, constant b is known as Wien's constant
Newton's Law of Cooling
Thermodynamics
If objects A and B are separately in thermal equilibrium with a third object C then objects A and B are in thermal equilibrium with each other.
If some quantity of heat is supplied to a system capable of doing external work, then the quantity of heat absorbed by the system is equal to the sum of the increase in the internal energy of the system and the external work done by the system.
i.e., \[\delta Q=\delta U+\delta W\]
The first law of thermodynamics is essentially a restatement of the law of conservation of energy, i.e., energy can neither be created nor be destroyed but may be converted from one form to another.
Equation of state: \[PV=\mu RT\]
Equation for adiabatic process \[P{{V}^{\gamma }}\] constant
Heat Engines
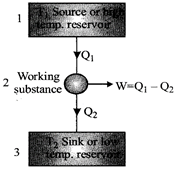
Efficiency of heat engine, \[\eta =\frac{Work\,\,done(W)}{Heat\,\,taken\,\,from\,\,soruce\,\,({{Q}_{1}})}\]\[\eta =\frac{{{T}_{1}}-{{T}_{2}}}{{{T}_{1}}}=\frac{{{Q}_{1}}-{{Q}_{2}}}{{{Q}_{1}}}=1-\frac{{{Q}_{2}}}{{{Q}_{1}}}\]
A refrigerator is the reverse of a heat engine. A heat pump is the same as a refrigerator.
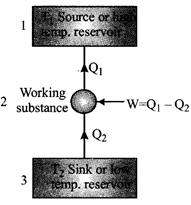
The coefficient of performance of a refrigerator or heat pump. \[\frac{{{Q}_{2}}}{W}=\frac{{{Q}_{2}}}{{{Q}_{1}}-{{Q}_{2}}}\] \[[\because W={{Q}_{1}}-{{Q}_{2}}]\]
No irreversible engine (I) can have efficiency greater than Carnot reversible engine (R) working between same hot and cold reservoirs. i.e., \[{{\eta }_{R}}>{{\eta }_{I}}\] or \[1-\frac{{{T}_{2}}}{{{T}_{1}}}>1-\frac{{{Q}_{2}}}{{{Q}_{1}}}\]
You need to login to perform this action.
You will be redirected in
3 sec
