JEE Main & Advanced Mathematics Vector Algebra Scalar or Dot Product

(1) Scalar or Dot product of two vectors : If \[\mathbf{a}\] and \[\mathbf{b}\] are two non-zero vectors and \[\theta \] be the angle between them, then their scalar product (or dot product) is denoted by \[\mathbf{a}\,.\,\mathbf{b}\] and is defined as the scalar \[|\mathbf{a}|\,|\mathbf{b}|\cos \theta \], where \[|\mathbf{a}|\,\text{ and }|\mathbf{b}|\]are modulii of \[\mathbf{a}\] and \[\mathbf{b}\] respectively and \[0\le \theta \le \pi \]. Dot product of two vectors is a scalar quantity.

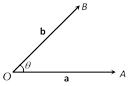
Angle between two vectors : If \[\mathbf{a},\,\mathbf{b}\] be two vectors inclined at an angle \[\theta \], then \[\mathbf{a}\,.\,\mathbf{b}=|\mathbf{a}|\,|\mathbf{b}|\,\cos \theta \]

\[\Rightarrow \] \[\cos \theta =\frac{\mathbf{a}\,.\,\mathbf{b}}{|\mathbf{a}|\,|\mathbf{b}|}\]\[\Rightarrow \] \[\theta ={{\cos }^{-1}}\left( \frac{\mathbf{a}\,.\,\mathbf{b}}{|\mathbf{a}|\,|\mathbf{b}|} \right)\]

If \[\mathbf{a}\,={{a}_{1}}\mathbf{i}+{{a}_{2}}\mathbf{j}+{{a}_{3}}\mathbf{k}\] and \[\mathbf{b}={{b}_{1}}\mathbf{i}+{{b}_{2}}\mathbf{j}+{{b}_{3}}\mathbf{k}\]; then

\[\theta ={{\cos }^{-1}}\left( \frac{{{a}_{1}}{{b}_{1}}+{{a}_{2}}{{b}_{2}}+{{a}_{3}}{{b}_{3}}}{\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}\sqrt{b_{1}^{2}+b_{2}^{2}+b_{3}^{2}}} \right)\].

(2) Properties of scalar product

(i) Commutativity : The scalar product of two vector is commutative i.e., \[\mathbf{a}\,.\,\mathbf{b}\,=\mathbf{b}\,.\,\mathbf{a}\].

(ii) Distributivity of scalar product over vector addition  The scalar product of vectors is distributive over vector addition i.e., (a) \[\mathbf{a}\,.\,(\mathbf{b}\,+\mathbf{c})\,=\,\mathbf{a}\,.\,\mathbf{b}+\mathbf{a}\,.\,\mathbf{c}\],     (Left distributivity) 

(b) \[(\mathbf{b}+\mathbf{c})\,.\,\mathbf{a}=\mathbf{b}\,.\,\mathbf{a}+\mathbf{c}\,.\,\mathbf{a}\],   (Right distributivity)

(iii) Let \[\mathbf{a}\] and \[\mathbf{b}\] be two non-zero vectors \[\mathbf{a}\,.\,\mathbf{b}=0\Leftrightarrow \mathbf{a}\bot \mathbf{b}\].

As \[\mathbf{i},\,\mathbf{j},\,\mathbf{k}\] are mutually perpendicular unit vectors along the co-ordinate axes, therefore, \[\mathbf{i}\,.\,\mathbf{j}=\mathbf{j}\,.\,\mathbf{i}=0\]; \[\mathbf{j}\,.\,\mathbf{k}=\mathbf{k}\,.\,\mathbf{j}=0;\] \[\mathbf{k}\,.\,\mathbf{i}=\mathbf{i}\,.\,\mathbf{k}\,=0\].

(iv) For any vector \[\mathbf{a},\,\text{ }\mathbf{a}\,.\,\mathbf{a}=|\mathbf{a}{{|}^{2}}\].

As \[\mathbf{i},\,\mathbf{j},\,\mathbf{k}\] are unit vectors along the co-ordinate axes, therefore \[\mathbf{i}\,.\,\mathbf{i}=|\mathbf{i}{{|}^{2}}=1\], \[\mathbf{j}\,.\,\mathbf{j}=|\mathbf{j}{{|}^{2}}=1\] and \[\mathbf{r}=\mathbf{a}+\lambda \mathbf{b}+\mu \mathbf{c}\]

(v) If m, n are scalars and \[\mathbf{a},\,\mathbf{b}\] be two vectors, then \[m\mathbf{a}\,.\,n\mathbf{b}=mn(\mathbf{a}\,.\,\mathbf{b})=(mn\,\mathbf{a})\,.\,\mathbf{b}=\mathbf{a}\,.\,(mn\,\mathbf{b})\]

(vi) For any vectors \[\mathbf{a}\] and \[\mathbf{b}\], we have

(a) \[\mathbf{a}\,.\ (-\mathbf{b})=-(\mathbf{a}\,.\,\mathbf{b})=(-\mathbf{a})\,.\,\mathbf{b}\]  

(b) \[(-\mathbf{a})\,.\,(-\mathbf{b})=\mathbf{a}\,.\,\mathbf{b}\]

(vii) For any two vectors \[\mathbf{a}\] and \[\mathbf{b}\], we have 

(a) \[|\mathbf{a}+\mathbf{b}{{|}^{2}}=\ |\mathbf{a}{{|}^{2}}+|\mathbf{b}{{|}^{2}}+\ 2\mathbf{a}\,.\,\mathbf{b}\]                

(b) \[|\mathbf{a}-\mathbf{b}{{|}^{2}}=\ |\mathbf{a}{{|}^{2}}+|\mathbf{b}{{|}^{2}}-\ 2\mathbf{a}\,.\,\mathbf{b}\]

(c) \[(\mathbf{a}+\mathbf{b})\,.\,(\mathbf{a}-\mathbf{b})=\ |\mathbf{a}{{|}^{2}}-|\mathbf{b}{{|}^{2}}\]                                 

(d) \[|\mathbf{a}+\mathbf{b}|\ =\ |\mathbf{a}|+|\mathbf{b}|\]\[\Rightarrow \] \[\mathbf{a}||\mathbf{b}\]

(e) \[|\mathbf{a}+\mathbf{b}{{|}^{2}}=\ |\mathbf{a}{{|}^{2}}+|\mathbf{b}{{|}^{2}}\Rightarrow \mathbf{a}\bot \mathbf{b}\]

(f) \[|\mathbf{a}+\mathbf{b}|\ =\ |\mathbf{a}-\mathbf{b}|\ \Rightarrow \mathbf{a}\bot \mathbf{b}\]

(3) Scalar product in terms of components: If \[\mathbf{a}={{a}_{1}}\mathbf{i}+{{a}_{2}}\mathbf{j}+{{a}_{3}}\mathbf{k}\] and \[\mathbf{b}={{b}_{1}}\mathbf{i}+{{b}_{2}}\mathbf{j}+{{b}_{3}}\mathbf{k}\], then, \[\mathbf{a}\,.\,\mathbf{b}={{a}_{1}}{{b}_{1}}\] \[+{{a}_{2}}{{b}_{2}}+{{a}_{3}}{{b}_{3}}\].

The components of \[\mathbf{b}\] along and perpendicular to \[\mathbf{a}\] are \[\left( \frac{\mathbf{a}\,.\ \mathbf{b}}{|\mathbf{a}{{|}^{2}}} \right)\,\mathbf{a}\] and \[\mathbf{b}-\left( \frac{\mathbf{a}\,.\,\mathbf{b}}{|\mathbf{a}{{|}^{2}}} \right)\,\mathbf{a}\] respectively.

(4) Work done by a force : 

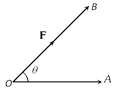
Work done \[=|\mathbf{F}|\,|\overrightarrow{OA}|\,\cos \theta =\mathbf{F}\,.\,\overrightarrow{OA}\,=\mathbf{F}\,.\mathbf{d}\], where \[\mathbf{d}=\overrightarrow{OA}\]

Work done = (Force). (Displacement)

If a number of forces are acting on a particle, then the sum of the works done by the separate forces is equal to the work done by the resultant force.