JEE Main & Advanced Mathematics Vector Algebra Vector or Cross Product

(1) Vector product of two vectors : Let \[\mathbf{a},\,\mathbf{b}\] be two non-zero, non-parallel vectors.

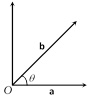
Then \[\mathbf{a}\times \mathbf{b}=|\mathbf{a}|\,|\mathbf{b}|\]\[\sin \theta \,\hat{\eta }\], and \[|\mathbf{a}\times \mathbf{b}|\text{ }=\text{ }|\mathbf{a}||\mathbf{b}|\sin \theta \], where \[\theta \] is the angle between \[\mathbf{a}\] and \[\mathbf{b}\], \[\hat{\eta }\] is a unit vector perpendicular to the plane of \[\mathbf{a}\] and \[\mathbf{b}\] such that \[\mathbf{a},\,\mathbf{b},\,\hat{\eta }\] form a right-handed system.

(2) Properties of vector product

(i) Vector product is not commutative i.e., if \[\mathbf{a}\] and \[\mathbf{b}\] are any two vectors, then \[\mathbf{a}\times \mathbf{b}\ne \mathbf{b}\times \mathbf{a}\], however, \[\mathbf{a}\times \mathbf{b}=-(\mathbf{b}\times \mathbf{a})\]

(ii) If \[\mathbf{a},\,\mathbf{b}\] are two vectors and m, n are scalars, then \[m\mathbf{a}\times n\mathbf{b}=mn(\mathbf{a}\times \mathbf{b})=m\,(\mathbf{a}\times n\mathbf{b})=n(m\,\mathbf{a}\times \mathbf{b})\].

(iii) Distributivity of vector product over vector addition.

Let \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\] be any three vectors. Then

(a) \[\mathbf{a}\times (\mathbf{b}+\mathbf{c})=\mathbf{a}\times \mathbf{b}+\mathbf{a}\times \mathbf{c}\]        (Left distributivity)

(b) \[(\mathbf{b}+\mathbf{c})\times \mathbf{a}=\mathbf{b}\times \mathbf{a}+\mathbf{c}\times \mathbf{a}\]        (Right distributivity)

(iv) For any three vectors \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\] we have \[\mathbf{a}\times (\mathbf{b}-\mathbf{c})=\] \[\mathbf{a}\times \mathbf{b}-\mathbf{a}\times \mathbf{c}\].

(v) The vector product of two non-zero vectors is zero vector iff they are parallel (Collinear) i.e., \[\mathbf{a}\times \mathbf{b}=0\Leftrightarrow \mathbf{a}||\mathbf{b},\,\mathbf{a},\,\mathbf{b}\] are non-zero vectors.

It follows from the above property that \[\mathbf{a}\times \mathbf{a}=0\] for every non-zero vector \[\mathbf{a}\], which in turn implies that \[\mathbf{i}\times \mathbf{i}=\] \[\mathbf{j}\times \mathbf{j}=\mathbf{k}\times \mathbf{k}=0\].

(vi) Vector product of orthonormal triad of unit vectors \[\mathbf{i},\text{ }\mathbf{j},\text{ }\mathbf{k}\] using the definition of the vector product, we obtain \[\mathbf{i}\times \mathbf{j}=\mathbf{k},\,\mathbf{j}\times \mathbf{k}=\mathbf{i},\,\mathbf{k}\times \mathbf{i}=\mathbf{j}\], \[\mathbf{j}\times \mathbf{i}=-\mathbf{k},\,\mathbf{k}\times \mathbf{j}=-\mathbf{i},\,\mathbf{i}\times \mathbf{k}=-\mathbf{j}\].

(3) Vector product in terms of components: If \[\mathbf{a}={{a}_{1}}\mathbf{i}+{{a}_{2}}\mathbf{j}+{{a}_{3}}\mathbf{k}\] and \[\mathbf{b}={{b}_{1}}\mathbf{i}+{{b}_{2}}\mathbf{j}+{{b}_{3}}\mathbf{k}\].

Then, \[\mathbf{a}\times \mathbf{b}=\left| \,\begin{matrix} \mathbf{i} & \mathbf{j} & \mathbf{k}  \\ {{a}_{1}} & {{a}_{2}} & {{a}_{3}}  \\ {{b}_{1}} & {{b}_{2}} & {{b}_{3}}  \\ \end{matrix}\, \right|\]

(4) Angle between two vectors : If \[\theta \] is the angle between \[\mathbf{a}\] and \[\mathbf{b}\], then \[\sin \theta =\frac{|\mathbf{a}\times \mathbf{b}|}{|\mathbf{a}|\,|\mathbf{b}|}\].

(5) (i) Right handed system of vectors : Three mutually perpendicular vectors \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\] form a right handed system of vector iff \[\mathbf{a}\times \mathbf{b}=\mathbf{c},\,\,\mathbf{b}\times \mathbf{c}=\mathbf{a},\,\,\mathbf{c}\times \mathbf{a}=\mathbf{b}\]

Examples: The unit vectors \[\mathbf{i}\,\mathbf{,}\,\mathbf{j,}\,\,\mathbf{k}\] form a right-handed system, \[\mathbf{i}\times \mathbf{j}=\mathbf{k},\,\mathbf{j}\times \mathbf{k}=\mathbf{i},\,\mathbf{k}\times \mathbf{i}=\mathbf{j}\]

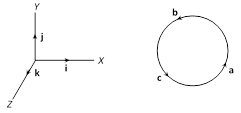
(ii) Left handed system of vectors : The vectors \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\] mutually perpendicular to one another form a left handed system of vector iff \[\mathbf{c}\times \mathbf{b}=\mathbf{a},\,\mathbf{a}\times \mathbf{c}=\mathbf{b},\mathbf{b}\times \mathbf{a}=\mathbf{c}\]

(6) Vector normal to the plane of two given vectors : If \[\mathbf{a},\,\mathbf{b}\] be two non-zero, nonparallel  vectors and let \[\theta \] be the angle between them. \[\mathbf{a}\times \mathbf{b}=|\mathbf{a}|\,|\mathbf{b}|\sin \theta \,\hat{\eta }\] where \[\hat{\eta }\] is a unit vector perpendicular to the plane of \[\mathbf{a}\] and \[\mathbf{b}\] such that \[\mathbf{a},\,\mathbf{b},\,\eta \] form a right-handed system.

\[\Rightarrow \]   \[(\mathbf{a}\times \mathbf{b})=|\mathbf{a}\times \mathbf{b}|\,\hat{\eta }\]\[\Rightarrow \] \[\hat{\eta }=\frac{\mathbf{a}\times \mathbf{b}}{|\mathbf{a}\times \mathbf{b}|}\]

Thus, \[\frac{\mathbf{a}\times \mathbf{b}}{|\mathbf{a}\times \mathbf{b}|}\] is a unit vector perpendicular to the plane of \[-\frac{\sqrt{3}}{2}\mathbf{i}+\frac{1}{2}\mathbf{j}\] and \[\mathbf{b}\]. Note that \[-\frac{\mathbf{a}\times \mathbf{b}}{|\mathbf{a}\times \mathbf{b}|}\] is also a unit vector perpendicular to the plane of \[\mathbf{a}\] and \[\mathbf{b}\]. Vectors of magnitude \['\lambda '\] normal to the plane of \[\mathbf{a}\] and \[\mathbf{b}\] are given by \[\pm \frac{\lambda (\mathbf{a}\times \mathbf{b})}{|\mathbf{a}\times \mathbf{b}|}\].

(7) Area of parallelogram and triangle

(i) The area of a parallelogram with adjacent sides \[\mathbf{a}\] and \[\mathbf{b}\] is \[|\mathbf{a}\times \mathbf{b}|\].

(ii) The area of a parallelogram with diagonals \[{{\mathbf{d}}_{1}}\] and \[{{\mathbf{d}}_{2}}\] is \[\frac{1}{2}|{{\mathbf{d}}_{1}}\times {{\mathbf{d}}_{2}}|\].

(iii) The area of a plane quadrilateral ABCD is \[\frac{1}{2}|\overrightarrow{AC}\times \overrightarrow{BD}|\], where AC and BD are its diagonals.

(iv) The area of a triangle with adjacent sides \[\mathbf{a}\] and \[\mathbf{b}\] is \[\frac{1}{2}|\mathbf{a}\times \mathbf{b}|\]

(v) The area of a triangle ABC is \[\frac{1}{2}|\overrightarrow{AB}\times \overrightarrow{AC}|\] or \[\frac{1}{2}|\overrightarrow{BC}\times \overrightarrow{BA}|\] or \[\frac{1}{2}|\overrightarrow{CB}\times \overrightarrow{CA}|\]

(vi) If \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\] are position vectors of vertices of a \[\Delta ABC,\] then its area \[=\frac{1}{2}|(\mathbf{a}\times \mathbf{b})\,+(\mathbf{b}\times \mathbf{c})+(\mathbf{c}\times \mathbf{a})|\]

(vii) Three points with position vectors \[\mathbf{a},\,\mathbf{b},\,\mathbf{c}\] are collinear if \[(\mathbf{a}\times \mathbf{b})\,+\,(\mathbf{b}\times \mathbf{c})+(\mathbf{c}\times \mathbf{a})=\mathbf{0}\].

(8) Moment of a force : Moment of a force \[\mathbf{F}\] about a point O is \[\overrightarrow{OP}\times \mathbf{F}\], where P is any point on the line of action of the force \[\mathbf{F}\].