Calculation of Necessary Force
Category : JEE Main & Advanced
Calculation of Necessary Force If W = weight of the body, \[\theta = angle of friction\], \[\mu =\tan \theta =\] coefficient of friction then we can calculate necessary force for different condition in the following manner: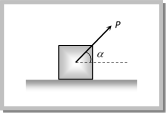 
(1) Minimum pulling force P at an angle a from the horizontal By resolving P in horizontal and vertical direction (as shown in figure) For the condition of equilibrium \[F=P\cos \alpha \] and \[R=W-P\sin \alpha \] By substituting these value in \[F=\mu R\] 
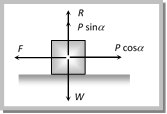\[P\cos \alpha =\mu \,(W-P\sin \alpha )\] \[\Rightarrow \,\,\,\,P\cos \alpha =\frac{\sin \theta }{\cos \theta }\,\,(W-P\sin \alpha )\] [As \[\mu =\tan \theta \]] \[\Rightarrow \,\,\,\,\,\,\,\,\,P=\frac{W\sin \theta }{\cos \,(\alpha -\theta )}\] (2) Minimum pushing force P at an angle a from the horizontal 
By Resolving P in horizontal and vertical direction (as shown in the figure) For the condition of equilibrium \[F=P\cos \alpha \] and \[R=W+P\sin \alpha \] By substituting these value in \[F=\mu R\]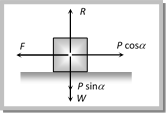 
\[\Rightarrow \,\,\,\,\,\,\,\,\,P\cos \alpha =\mu \,(W+P\sin \alpha )\] \[\Rightarrow \,\,\,\,\,P\cos \alpha =\frac{\sin \theta }{\cos \theta }\,(W+P\sin \alpha )\,\,\,\,[As\,\,\mu =\tan \theta ]\] \[\Rightarrow \,\,\,\,\,\,\,\,\,P=\frac{W\sin \theta }{\cos \,(\alpha +\theta )}\] (3) Minimum pulling force P to move the body up an inclined plane By Resolving P in the direction of the plane and perpendicular to the plane (as shown in the figure) For the condition of equilibrium 
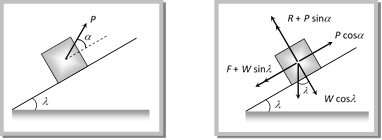\[R+P\sin \alpha =W\cos \lambda \] \[\therefore \,\,\,\,\,\,\,\,\,\,\,\,R=W\cos \lambda -P\,\sin \alpha \] and \[F+W\sin \lambda =P\cos \alpha \] \[\therefore \,\,\,\,\,\,\,\,\,F=P\cos \alpha -W\sin \lambda \] By substituting these values in \[F=\mu R\] and solving we get \[P=\frac{W\sin \,(\theta +\lambda )}{\cos \,(\alpha -\theta )}\] (4) Minimum force on body in downward direction along the surface of inclined plane to start its motion By Resolving P in the direction of the plane and perpendicular to the plane (as shown in the figure) For the condition of equilibrium 
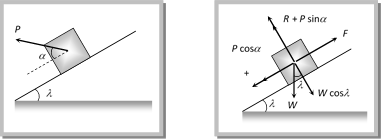\[R+P\sin \alpha =W\cos \lambda \] \[\therefore \,\,\,\,\,\,\,\,\,\,\,\,R=W\cos \lambda -P\sin \alpha \] and \[F=P\cos \alpha +W\sin \lambda \] By substituting these values in \[F=\mu R\] and solving we get \[P=\frac{W\sin (\theta -\lambda )}{\cos \,(\alpha -\theta )}\] (5) Minimum force to avoid sliding a body down an inclined plane By Resolving P in the direction of the plane and perpendicular to the plane (as shown in the figure) 
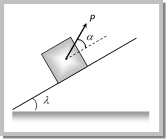For the condition of equilibrium 
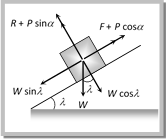\[R+P\sin \alpha =W\cos \lambda \] \[\therefore \,\,\,\,\,\,\,\,\,\,\,R=W\cos \lambda -P\sin \alpha \] and \[P\cos \alpha +F=W\sin \lambda \] \ \[F=W\sin \lambda -P\cos \alpha \] By substituting these values in \[F=\mu R\] and solving we get \[P=W\,\left[ \frac{\sin \,(\lambda -\theta )}{\cos \,(\theta +\alpha )} \right]\] (6) Minimum force for motion and its direction 
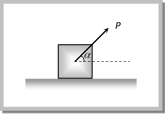Let the force P be applied at an angle\[\alpha \]with the horizontal. By resolving P in horizontal and vertical direction (as shown in figure) For vertical equilibrium \[R+P\sin \alpha =mg\] \[\therefore \,\,\,\,\,\,\,\,\,\,\,R=mg-P\sin \alpha \] ?. (i) and for horizontal motion 
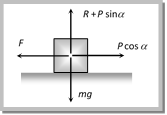\[P\cos \alpha \ge F\] i.e. \[P\cos \alpha \ge \mu R\] ?. (ii) Substituting value of R from (i) in (ii) \[P\cos \alpha \ge \mu \,(mg-P\sin \alpha )\] \[P\ge \frac{\mu \,mg}{\cos \alpha +\mu \sin \alpha }\] ?. (iii) For the force P to be minimum \[(\cos \alpha +\mu \sin \alpha )\] must be maximum i.e. \[\frac{d}{d\alpha }[\cos \alpha +\mu \sin \alpha ]=0\Rightarrow -\sin \alpha +\mu \cos \alpha =0\] \[\therefore \,\,\,\,\,\,\,\tan \alpha =\mu \] or \[\alpha ={{\tan }^{-1}}(\mu )=\text{angle of friction }\] i.e. For minimum value of P its angle from the horizontal should be equal to angle of friction 
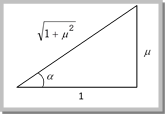As \[\tan \alpha =\mu \] so from the figure \[\sin \alpha =\frac{\mu }{\sqrt{1+{{\mu }^{2}}}}\] and \[\cos \alpha =\frac{1}{\sqrt{1+{{\mu }^{2}}}}\] By substituting these value in equation (iii) \[P\ge \frac{\mu \,mg}{\frac{1}{\sqrt{1+{{\mu }^{2}}}}+\frac{{{\mu }^{2}}}{\sqrt{1+{{\mu }^{2}}}}}\ge \frac{\mu \,mg}{\sqrt{1+{{\mu }^{2}}}}\] \[\therefore \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{P}_{\min }}=\frac{\mu mg}{\sqrt{1+{{\mu }^{2}}}}\] Sample problems based on force against friction Problem 9. What is the maximum value of the force F such that the block shown in the arrangement, does not move (\[\mu =1/2\sqrt{3}\]) [IIT-JEE (Screening) 2003] 
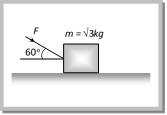(a) 20 N (b) 10 N (c) 12 N (d) 15 N Solution: (a) Frictional force \[f=\mu R\] \[\Rightarrow \,\,F\cos 60=\mu (W+F\sin 60)\] 
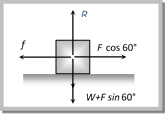\[\Rightarrow \,\,\,F\cos 60=\frac{1}{2\sqrt{3}}\,\,\left( \sqrt{3}g+F\sin \,\,60 \right)\] \[\Rightarrow \,\,\,F=20\,N\] Problem 10. A block of mass m rests on a rough horizontal surface as shown in the figure. Coefficient of friction between the block and the surface is m. A force F = mg acting at angle \[\theta \] with the vertical side of the block pulls it. In which of the following cases the block can be pulled along the surface 
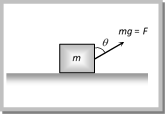(a) \[\tan \theta \ge \mu \] (b) \[\cot \theta \ge \mu \] (c) \[\tan \theta /2\ge \mu \] (d) \[\cot \theta /2\ge \mu \] Solution: (d) For pulling of block \[P\ge f\] 
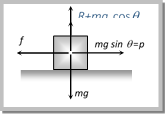\[\Rightarrow \,\,\,mg\,\sin \theta \ge \mu R\Rightarrow mg\sin \theta \ge \,\mu \,(mg-mg\cos \theta )\] \[\Rightarrow \,\,\sin \theta \ge \,\mu \,(1-\cos \theta )\] \[\Rightarrow \,\,\,2\sin \frac{\theta }{2}\cos \frac{\theta }{2}\ge \mu \,\left( 2{{\sin }^{2}}\frac{\theta }{2} \right)\Rightarrow \cot \left( \frac{\theta }{2} \right)\ge \mu \]
You need to login to perform this action.
You will be redirected in
3 sec
