JEE Main & Advanced Physics NLM, Friction, Circular Motion Friction is a Cause of Motion

Friction is a Cause of Motion It is a general misconception that friction always opposes the motion. No doubt friction opposes the motion of a moving body but in many cases it is also the cause of motion. For example: (1) In moving, a person or vehicle pushes the ground backwards (action) and the rough surface of ground reacts and exerts a forward force due to friction which causes the motion. If there had been no friction there will be slipping and no motion. 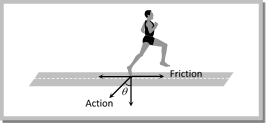(2) In cycling, the rear wheel moves by the force communicated to it by pedalling while front wheel moves by itself. So, when pedalling a bicycle, the force exerted by rear wheel on ground makes force of friction act on it in the forward direction (like walking). Front wheel moving by itself experience force of friction in backward direction (like rolling of a ball). [However, if pedalling is stopped both wheels move by themselves and so experience force of friction in backward direction.] 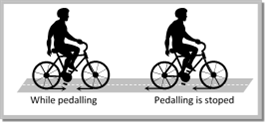(3) If a body is placed in a vehicle which is accelerating, the force of friction is the cause of motion of the body along with the vehicle (i.e., the body will remain at rest in the accelerating vehicle until \[ma<{{\mu }_{s}}mg).\] If there had been no friction between body and vehicle the body will not move along with the vehicle. 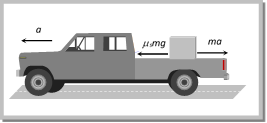From these examples it is clear that without friction motion cannot be started, stopped or transferred from one body to the other. Sample problems based on fundamentals of friction Problem 1. If a ladder weighing 250 N is placed against a smooth vertical wall having coefficient of friction between it and floor is 0.3, then what is the maximum force of friction available at the point of contact between the ladder and the floor [AIIMS 2002] (a) 75 N             (b) 50 N             (c) 35 N             (d) 25 N Solution: (a) Maximum force of friction \[{{F}_{l}}={{\mu }_{s}}R=0.3\times 250=75\,N\] Problem 2. On the horizontal surface of a truck \[(\mu = 0.6)\], a block of mass 1 kg is placed.  If the truck is accelerating at the rate of \[5m/se{{c}^{2}}\] then frictional force on the block will be [CBSE PMT 2001] (a) 5 N             (b) 6 N              (c) 5.88 N          (d) 8 N Solution: (a) Limiting friction \[={{\mu }_{s}}R={{\mu }_{s}}mg=0.6\times 1\times 9.8=5.88\,N\] When truck accelerates in forward direction at the rate of \[5m/{{s}^{2}}\] a pseudo force \[(ma)\] of 5N works on block in back ward direction. Here the magnitude of pseudo force is less than limiting friction So, static friction works in between the block and the surface of the truck and as we know, static friction = Applied force = 5 N. Problem 3. A block of mass 2 kg is kept on the floor. The coefficient of static friction is 0.4. If a force F of 2.5 N is applied on the block as shown in the figure, the frictional force between the block and the floor will be [MP PET 2000] (a) 2.5 N                                    (b) 5 N (c) 7.84 N                                  (d) 10 N Solution: (a) Applied force = 2.5 N and limiting friction = mmg \[= 0.4 \,\times \, 2 \,\times \, 9.8 = 7.84 N\] As applied force is less than limiting friction. So, for the given condition static friction will work. Static friction on a body = Applied force = 2.5 N. Problem 4. A block A with mass 100 kg is resting on another block B of mass 200 kg. As shown in figure a horizontal rope tied to a wall holds it.  The coefficient of friction between A and B is 0.2 while coefficient of friction between B and the ground is 0.3. The minimum required force F to start moving B will be [RPET 1999] 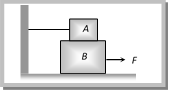(a) 900 N                       (b) 100 N (c) 1100 N                     (d) 1200 N Solution: (c) Two frictional force will work on block B. \[F={{f}_{AB}}+{{f}_{BG}}\]\[={{\mu }_{AB}}{{m}_{a}}g+{{\mu }_{BG}}({{m}_{A}}+{{m}_{B}})g\]  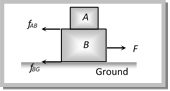   \[= 0.2 \times  100 \times  10 + 0.3 \left( 300 \right) \times  10\]     \[= 200 + 900 = 1100N.\] (This is the required minimum force) Problem 5. A 20 kg block is initially at rest on a rough horizontal surface. A horizontal force of 75 N is required to set the block in motion. After it is in motion, a horizontal force of 60 N is required to keep the block moving with constant speed.  The coefficient of static friction is [AMU 1999] (a) 0.38             (b) 0.44             (c) 0.52             (d) 0.60 Solution: (a) Coefficient of static friction \[{{\mu }_{S}}=\frac{{{F}_{l}}}{R}=\frac{75}{20\times 9.8}=0.38\]. Problem 6. A block of mass M is placed on a rough floor of a lift. The coefficient of friction between the block and the floor is \[\mu \]. When the lift falls freely, the block is pulled horizontally on the floor. What will be the force of friction (a) \[\mu \,Mg\]   (b) \[\mu \,Mg/2\]            (c) \[2\,\mu \,Mg\]           (d) None of these Solution: (d) When the lift moves down ward with acceleration 'a' then effective acceleration due to gravity g' = g ? a  \[\therefore \,\,\,\,\,\,g'\,=g-g=0\] [As the lift falls freely, so a = g] So force of friction \[=\mu mg'=0\]