JEE Main & Advanced Physics Ray Optics Lens Immersed in a Liquid

If a lens (made of glass) of refractive index \[{{\mu }_{g}}\] is immersed in a liquid of refractive index \[{{\mu }_{l}}\], then its focal length in liquid, \[{{f}_{l}}\] is given by        \[\frac{1}{{{f}_{l}}}=({{\,}_{l}}{{\mu }_{g}}-1)\,\left( \frac{1}{{{R}_{1}}}-\frac{1}{{{R}_{2}}} \right)\]                    ......(i)

If \[{{f}_{a}}\] is the focal length of lens in air, then

\[\frac{1}{{{f}_{a}}}=({{\,}_{a}}{{\mu }_{g}}-1)\,\left( \frac{1}{{{R}_{1}}}-\frac{1}{{{R}_{2}}} \right)\]                 ......(ii)

\[\Rightarrow \]\[\frac{{{f}_{l}}}{{{f}_{a}}}=\frac{{{(}_{a}}{{\mu }_{g}}-1)}{{{(}_{l}}{{\mu }_{g}}-1)}\] (1) If \[{{\mu }_{g}}>{{\mu }_{l}},\] then \[{{f}_{l}}\] and \[{{f}_{a}}\] are of same sign and \[{{f}_{l}}>{{f}_{a}}\].

That is the nature of lens remains unchanged, but it's focal length increases and hence power of lens decreases.

(2) If \[{{\mu }_{g}}={{\mu }_{l}},\] then \[{{f}_{l}}=\infty \]. It means lens behaves as a plane glass plate and becomes invisible in the medium.

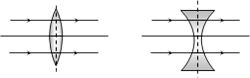
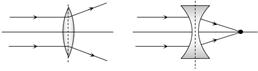
(3) If \[{{\mu }_{g}}<{{\mu }_{l}},\] then \[{{f}_{l}}\] and \[{{f}_{a}}\] have opposite signs and the nature of lens changes i.e. a convex lens diverges the light rays and concave lens converges the light rays.