JEE Main & Advanced Physics Ray Optics Microscope

It is an optical instrument used to see very small objects. It's magnifying power is given by

\[m=\frac{\text{Visual angle with instrument(}\beta \text{)}}{\text{Visual angle when object is placed at least distance of distinct vision (}\alpha \text{)}}\]

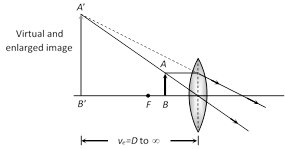
(1) Simple microscope

(i) It is a single convex lens of lesser focal length.

(ii) Also called magnifying glass or reading lens.

(iii) Magnification's, when final image is formed at D and \[\infty \]

(i.e. \[{{m}_{D}}\] and \[{{m}_{\infty }}\])      \[{{m}_{D}}={{\left( 1+\frac{D}{f} \right)}_{\max }}\] and \[{{m}_{\infty }}={{\left( \frac{D}{f} \right)}_{\min }}\]

(iv) If lens is kept at a distance a from the eye then \[{{m}_{D}}=1+\frac{D-a}{f}\] and \[{{m}_{\infty }}=\frac{D-a}{f}\]

(2) Compound microscope

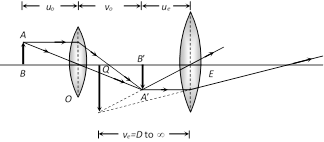
(i) Consist of two converging lenses called objective and eye lens.

(ii) \[{{f}_{\text{eye lens}}}>{{f}_{\text{objective}}}\]and \[{{(\text{diameter)}}_{\text{eye lens}}}>{{(\text{diameter})}_{\text{objective}}}\]

(iii) Intermediate image is real and enlarged.

(iv) Final image is magnified, virtual and inverted.

(v) \[{{u}_{o}}=\]Distance of object from objective (o), \[{{v}_{o}}=\]Distance of image \[({A}'{B}')\] formed by objective from objective, \[{{u}_{e}}=\] Distance of \[{A}'{B}'\] from eye lens, \[{{v}_{e}}=\] Distance of final image from eye lens, \[{{f}_{o}}=\] Focal length of objective, \[{{f}_{e}}=\] Focal length of eye lens.

(vi) Final image is formed at D : Magnification \[{{m}_{D}}=-\frac{{{v}_{o}}}{{{u}_{o}}}\left( 1+\frac{D}{{{f}_{e}}} \right)\] and length of the microscope tube (distance between two lenses) is \[{{L}_{D}}={{v}_{o}}+{{u}_{e}}\].

Generally object is placed very near to the principal focus of the objective hence \[{{u}_{o}}\tilde{=}\,{{f}_{o}}.\] The eye piece is also of small focal length and the image formed by the objective is also very near to the eye piece.

So \[{{v}_{o}}\tilde{=}{{L}_{D}},\] the length of the tube.

Hence, we can write \[{{m}_{D}}=\frac{-L}{{{f}_{o}}}\,\left( 1+\frac{D}{{{f}_{e}}} \right)\]

(vii) Final image is formed at \[\infty \] : Magnification

\[{{m}_{\infty }}=-\frac{{{v}_{0}}}{{{u}_{0}}}.\frac{D}{{{f}_{e}}}\]and length of tube \[{{L}_{\infty }}={{v}_{0}}+{{f}_{e}}\]  

In terms of length \[{{m}_{\infty }}=\frac{({{L}_{\infty }}-{{f}_{o}}-{{f}_{e}})D}{{{f}_{o}}{{f}_{e}}}\]

(viii) For large magnification of the compound microscope, both \[{{f}_{o}}\] and \[{{f}_{e}}\] should be small.

(ix) If the length of the tube of microscope increases, then its magnifying power increases.

(x) The magnifying power of the compound microscope may be expressed as \[M={{m}_{o}}\times {{m}_{e}}\]; where  \[{{m}_{o}}\] is the magnification of the objective and \[{{m}_{e}}\] is magnifying power of eye piece.