JEE Main & Advanced Physics Ray Optics Prism

Prism is a transparent medium bounded by refracting surfaces, such that the incident surface (on which light ray is incidenting) and emergent surface (from which light rays emerges) are plane and non parallel.

(1) Refraction through a prism 

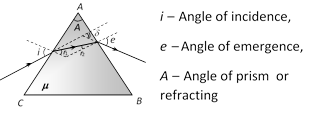
\[A={{r}_{1}}+{{r}_{2}}\] and \[i+e=A+\delta \]

For surface \[AC\,\,\mu =\frac{\sin i}{\sin {{r}_{1}}}\]; For surface AB \[\frac{1}{\mu }=\frac{\sin {{r}_{2}}}{\sin e}\]

(2) Deviation through a prism : For thin prism \[\delta =(\mu -1)A\]. Also deviation is different for different colour light e.g.\[{{\mu }_{R}}<{{\mu }_{V}}\] so \[{{\delta }_{R}}<{{\delta }_{V}}\].

\[{{\mu }_{\text{Flint}}}>{{\mu }_{\text{Crown}}}\] so \[{{\delta }_{F}}>{{\delta }_{C}}\]

(i) Maximum deviation : Condition of maximum deviation is \[\angle \,i={{90}^{o}}\]\[\Rightarrow \]\[{{r}_{1}}=C,\]\[{{r}_{2}}=A-C\] and from Snell's law on emergent surface

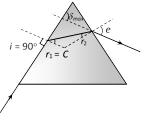
\[e={{\sin }^{-1}}\left[ \frac{\sin (A-C)}{\sin \,C} \right]\]

\[{{\delta }_{\max }}=\frac{\pi }{2}+{{\sin }^{-1}}\left[ \frac{\sin (A-C)}{\sin C} \right]-A\]

(ii) Minimum deviation : It is observed if \[\angle i=\angle e\] and \[\angle {{r}_{1}}=\angle {{r}_{2}}=r\], deviation produced is minimum.

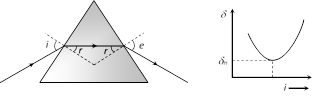
(a) Refracted ray inside the prism is parallel to the base of the prism for equilateral and isosceles prisms.  

(b)  \[r=\frac{A}{2}\]  and \[i=\frac{A+{{\delta }_{m}}}{2}\]

(c)  \[\mu =\frac{\sin \,i}{\sin \,A/2}\] or \[\mu =\frac{\sin \frac{A+{{\delta }_{m}}}{2}}{\sin A/2}\]   (Prism formula).

(3) Condition of no emergence : For no emergence of light, TIR must takes place at the second surface

For TIR at second surface \[{{r}_{2}}>C\]  

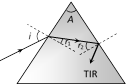
So \[A>{{r}_{1}}+C\] (From \[A={{r}_{1}}+{{r}_{2}}\])

As maximum value of \[{{r}_{1}}=C\]

So, \[A\ge 2C.\] for any angle of incidence.

If light ray incident normally on first surface i.e. \[\angle i={{0}^{o}}\] it means \[\angle {{r}_{1}}={{0}^{o}}\]. So in this case condition of no emergence from second surface is \[A>C\].

\[\Rightarrow \]\[\sin A>\sin C\]\[\Rightarrow \] \[\sin A>\frac{1}{\mu }\]\[\Rightarrow \] \[\mu >\text{cosec}\,A\]