Atomic Models and Plancks Quantum Theory
Category : NEET
Atomic Models and Planck's Quantum Theory
Atomic spectrum - Hydrogen spectrum.
Atomic spectrum
(1) Spectrum is the impression produced on a photographic film when the radiation (s) of particular wavelength (s) is (are) analysed through a prism or diffraction grating. It is of two types, emission and absorption.
(2) Emission spectrum : A substance gets excited on heating at a very high temperature or by giving energy and radiations are emitted. These radiations when analysed with the help of spectroscope, spectral lines are obtained. A substance may be excited, by heating at a higher temperature, by passing electric current at a very low pressure in a discharge tube filled with gas and passing electric current into metallic filament. Emission spectra is of two types,
(i) Continuous spectrum : When sunlight is passed through a prism, it gets dispersed into continuous bands of different colours. If the light of an incandescent object resolved through prism or spectroscope, it also gives continuous spectrum of colours.
(ii) Line spectrum : If the radiations obtained by the excitation of a substance are analysed with help of a spectroscope a series of thin bright lines of specific colours are obtained. There is dark space in between two consecutive lines. This type of spectrum is called line spectrum or atomic spectrum..
(3) Absorption spectrum : When the white light of an incandescent substance is passed through any substance, this substance absorbs the radiations of certain wavelength from the white light. On analysing the transmitted light we obtain a spectrum in which dark lines of specific wavelengths are observed. These lines constitute the absorption spectrum. The wavelength of the dark lines correspond to the wavelength of light absorbed.
Hydrogen spectrum
(1) Hydrogen spectrum is an example of line emission spectrum or atomic emission spectrum.
(2) When an electric discharge is passed through hydrogen gas at low pressure, a bluish light is emitted.
(3) This light shows discontinuous line spectrum of several isolated sharp lines through prism.
(4) All these lines of H-spectrum have Lyman, Balmer, Paschen, Barckett, Pfund and Humphrey series. These spectral series were named by the name of scientist discovered them.
(5) To evaluate wavelength of various H-lines Ritz introduced the following expression,
\[\bar{\nu }=\frac{1}{\lambda }=\frac{\nu }{c}=R\left[ \frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}} \right]\]
Where R is universal constant known as Rydberg’s constant its value is 109, 678\[c{{m}^{-1}}\].
Thomson's model.
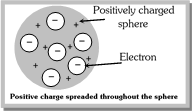
(1) Thomson regarded atom to be composed of positively charged protons and negatively charged electrons. The two types of particles are equal in number thereby making atom electrically neutral.
(2) He regarded the atom as a positively charged sphere in which negative electrons are uniformly distributed like the seeds in a water melon.
(3) This model failed to explain the line spectrum of an element and the scattering experiment of Rutherford.
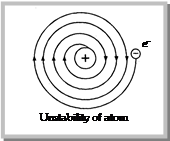
(2) From the above observations he concluded that, an atom consists of
(i) Nucleus which is small in size but carries the entire mass i.e. contains all the neutrons and protons.
(ii) Extra nuclear part which contains electrons. This model was similar to the solar system.

(2) From the above observations he concluded that, an atom consists of
(i) Nucleus which is small in size but carries the entire mass i.e. contains all the neutrons and protons.
(ii) Extra nuclear part which contains electrons. This model was similar to the solar system.

(3) Properties of the Nucleus
(i) Nucleus is a small, heavy, positively charged portion of the atom and located at the centre of the atom.
(ii) All the positive charge of atom (i.e. protons) are present in nucleus.
(iii) Nucleus contains neutrons and protons, and hence these particles collectively are also referred to as nucleons.
(iv) The size of nucleus is measured in Fermi (1 Fermi = 10–13 cm).
(v) The radius of nucleus is of the order of \[1.5\times {{10}^{-13}}cm.\] to \[6.5\times {{10}^{-13}}cm.\] i.e. \[1.5\] to \[6.5\] Fermi. Generally the radius of the nucleus (\[{{r}_{n}})\] is given by the following relation,
![]()
This exhibited that nucleus is \[{{10}^{-5}}\] times small in size as compared to the total size of atom.
(vi) The Volume of the nucleus is about \[{{10}^{-39}}\]\[c{{m}^{3}}\] and that of atom is \[{{10}^{-24}}c{{m}^{3}},\] i.e., volume of the nucleus is \[{{10}^{-15}}\] times that of an atom.
(vii) The density of the nucleus is of the order of \[{{10}^{15}}g\,c{{m}^{-3}}\] or \[{{10}^{8}}\] tonnes \[c{{m}^{-3}}\] or \[{{10}^{12}}kg/cc\]. If nucleus is spherical than,
Density =\[\frac{\text{mass of the nucleus}}{\text{volume of the nucleus }}=\]\[\frac{\text{mass number}}{6.023\times {{10}^{23}}\times \frac{4}{3}\pi {{r}^{3}}}\]
(4) Drawbacks of Rutherford's model
(i) It does not obey the Maxwell theory of electrodynamics, according to it “A small charged particle moving around an oppositely charged centre continuously loses its energy”. If an electron does so, it should also continuously lose its energy and should set up spiral motion ultimately failing into the nucleus.
(ii) It could not explain the line spectra of \[H-\] atom and discontinuous spectrum nature.
Examples based on Properties of the nucleus
Example:14 Assuming a spherical shape for fluorine nucleus, calculate the radius and the nuclear density of fluorine nucleus of mass number 19.
Solution : We know that,
\[r=(1.4\times {{10}^{-13}}){{A}^{1/3}}\] \[=1.4\times {{10}^{-13}}\times {{19}^{1/3}}\] \[=3.73\times {{10}^{-13}}cm\] (A for F=19)
Volume of a fluorine atom\[=\frac{4}{3}\pi {{r}^{3}}\] \[=\frac{4}{3}\times 3.14\times {{(3.73\times {{10}^{-13}})}^{3}}\] \[=2.18\times {{10}^{-37}}c{{m}^{3}}\]
\[\text{Mass of single nucleus }=\frac{\text{Mass of one mol of nucleus}}{\text{Avogadro }\!\!'\!\!\text{ s number}}\]\[=\frac{19}{6.023\times {{10}^{23}}}g\]
Thus\[\text{Density of nucleus }=\frac{\text{Mass of single nucleus}}{\text{Volume of single nucleus }}\]\[=\frac{10}{6.023\times {{10}^{23}}}\times \frac{1}{2.18\times {{10}^{-37}}}\] \[=7.616={{10}^{13}}g\,c{{m}^{-1}}\]
Example: 15 Atomic radius is the order of \[{{10}^{-8}}cm,\]and nuclear radius is the order of \[{{10}^{-13}}cm.\]Calculate what fraction of atom is occupied by nucleus.
Solution : Volume of nucleus\[=(4/3)p{{r}^{3}}\] \[=(4/3)p\times {{({{10}^{-13}})}^{3}}c{{m}^{3}}\]
Volume of atom\[=(4/3)p{{r}^{3}}=(4/3)p\times {{({{10}^{-8}})}^{3}}c{{m}^{3}}\]
\[\therefore \] \[\frac{{{V}_{nucleus}}}{{{V}_{atom}}}=\frac{{{10}^{-39}}}{{{10}^{-24}}}={{10}^{-15}}\] or \[{{V}_{nucleus}}={{10}^{-15}}\times {{V}_{atom}}\]
Planck's Quantum theory and Photoelectric effect.
Planck's Quantum theory
(1) Max Planck (1900) to explain the phenomena of 'Black body radiation' and 'Photoelectric effect' gave quantum theory. This theory extended by Einstein (1905).
(2) If the substance being heated is a black body (which is a perfect absorber and perfect radiator of energy) the radiation emitted is called black body radiation.
(3) Main points
(i) The radiant energy which is emitted or absorbed by the black body is not continuous but discontinuous in the form of small discrete packets of energy, each such packet of energy is called a 'quantum'. In case of light, the quantum of energy is called a 'photon'.
(ii) The energy of each quantum is directly proportional to the frequency (\[\nu \]) of the radiation, i.e.
\[E\propto \nu \] or \[E=hv=\frac{hc}{\lambda }\]
where, \[h=\] Planck's constant = 6.62×10–27 erg. sec. or \[6.62\times {{10}^{-34}}Joules\,\sec .\]
(iii) The total amount of energy emitted or absorbed by a body will be some whole number quanta. Hence \[E=nh\nu ,\] where n is an integer.
(iv) The greater the frequency (i.e. shorter the wavelength) the greater is the energy of the radiation.
thus, \[\frac{{{E}_{1}}}{{{E}_{2}}}=\frac{{{\nu }_{1}}}{{{\nu }_{2}}}=\frac{{{\lambda }_{2}}}{{{\lambda }_{1}}}\]
(v) Also \[E={{E}_{1}}+{{E}_{2}},\] hence, \[\frac{hc}{\lambda }=\frac{hc}{{{\lambda }_{1}}}+\frac{hc}{{{\lambda }_{2}}}\] or \[\frac{1}{\lambda }=\frac{1}{{{\lambda }_{1}}}+\frac{1}{{{\lambda }_{2}}}\].
Examples based on Planck's Quantum theory
Example: 16 Suppose \[{{10}^{-17}}J\] of energy is needed by the interior of human eye to see an object. How many photons of green light \[(\lambda =550\,nm)\] are needed to generate this minimum amount of energy?
(a) 14 (b) 28 (c) 39 (d) 42
Solution : (b) Let the number of photons required =n
\[n\frac{hc}{\lambda }={{10}^{-17}}\]; \[n=\frac{{{10}^{-17}}\times \lambda }{hc}=\frac{{{10}^{-17}}\times 550\times {{10}^{-9}}}{6.626\times {{10}^{-34}}\times 3\times {{10}^{8}}}=27.6=28\] photons
Example: 17 Assuming that a 25 watt bulb emits monochromatic yellow light of wave length \[0.57\mu .\] The rate of emission of quanta per sec. will be
(a) \[5.89\times {{10}^{13}}{{\sec }^{-1}}\] (b) \[7.28\times {{10}^{17}}{{\sec }^{-1}}\] (c) \[5\times {{10}^{10}}{{\sec }^{-1}}\] (d) \[7.18\times {{10}^{19}}{{\sec }^{-1}}\]
Solution: (d) Let n quanta are evolved per sec.
\[n\left[ \frac{hc}{\lambda } \right]=25J\,{{\sec }^{-1}}\]; \[n\frac{6.626\times {{10}^{-34}}\times 3\times {{10}^{8}}}{0.57\times {{10}^{-6}}}=25\]; \[n=7.18\times {{10}^{19}}{{\sec }^{-1}}\]
Photoelectric effect
(1) When radiations with certain minimum frequency \[({{\nu }_{0}})\] strike the surface of a metal, the electrons are ejected from the surface of the metal. This phenomenon is called photoelectric effect and the electrons emitted are called photo-electrons. The current constituted by photoelectrons is known as photoelectric current.
(2) The electrons are ejected only if the radiation striking the surface of the metal has at least a minimum frequency \[({{\nu }_{0}})\] called Threshold frequency. The minimum potential at which the plate photoelectric current becomes zero is called stopping potential.
(3)The velocity or kinetic energy of the electron ejected depend upon the frequency of the incident radiation and is independent of its intensity.
(4) The number of photoelectrons ejected is proportional to the intensity of incident radiation.
(5) Einstein’s photoelectric effect equation : According to Einstein,
Maximum kinetic energy of the ejected electron = absorbed energy – threshold energy
\[\frac{1}{2}mv_{\max }^{2}=h\nu -h{{\nu }_{0}}=hc\left[ \frac{1}{\lambda }-\frac{1}{{{\lambda }_{0}}} \right]\]
where, \[{{\nu }_{0}}\] and \[{{\lambda }_{0}}\] are threshold frequency and threshold wavelength.
![]() Note : q Nearly all metals emit photoelectrons when exposed to u.v. light. But alkali metals like lithium, sodium, potassium, rubidium and caesium emit photoelectrons even when exposed to visible light.
Note : q Nearly all metals emit photoelectrons when exposed to u.v. light. But alkali metals like lithium, sodium, potassium, rubidium and caesium emit photoelectrons even when exposed to visible light.
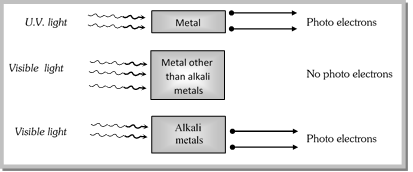
Caesium (Cs) with lowest ionisation energy among alkali metals is used in photoelectric cell.
Bohr’s atomic model.
(1) This model was based on the quantum theory of radiation and the classical law of physics. It gave new idea of atomic structure in order to explain the stability of the atom and emission of sharp spectral lines.
(2) Postulates of this theory are :
(i) The atom has a central massive core nucleus where all the protons and neutrons are present. The size of the nucleus is very small.
(ii) The electron in an atom revolve around the nucleus in certain discrete orbits. Such orbits are known as stable orbits or non – radiating or stationary orbits.
(iii) The force of attraction between the nucleus and the electron is equal to centrifugal force of the moving electron.
Force of attraction towards nucleus = centrifugal force
(iv) An electron can move only in those permissive orbits in which the angular momentum (mvr) of the electron is an integral multiple of \[h/2\pi .\]Thus, \[\text{mvr}=n\frac{\text{h}}{\text{2}\pi }\]
Where, m = mass of the electron, r = radius of the electronic orbit, v = velocity of the electron in its orbit.
(v) The angular momentum can be \[\frac{h}{2\pi },\,\frac{2h}{2\pi },\,\frac{3h}{2\pi },......\frac{nh}{2\pi }.\] This principal is known as quantization of angular momentum. In the above equation ‘n’ is any integer which has been called as principal quantum number. It can have the values n=1,2,3, ------- (from the nucleus). Various energy levels are designed as K(n=1), L(n=2), M(n=3) ------- etc. Since the electron present in these orbits is associated with some energy, these orbits are called energy levels.
(vi) The emission or absorption of radiation by the atom takes place when an electron jumps from one stationary orbit to another.

(vii) The radiation is emitted or absorbed as a single quantum (photon) whose energy \[h\nu \]is equal to the difference in energy \[\Delta E\]of the electron in the two orbits involved. Thus, \[h\nu =\Delta E\]
Where ‘h’ =Planck’s constant, \[\nu =\]frequency of the radiant energy. Hence the spectrum of the atom will have certain fixed frequency.
(viii) The lowest energy state (n=1) is called the ground state. When an electron absorbs energy, it gets excited and jumps to an outer orbit. It has to fall back to a lower orbit with the release of energy.
(3) Advantages of Bohr’s theory
(i) Bohr’s theory satisfactorily explains the spectra of species having one electron, viz. hydrogen atom, \[H{{e}^{+}},L{{i}^{2+}}\]etc.
(ii) Calculation of radius of Bohr’s orbit : According to Bohr, radius of orbit in which electron moves is
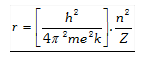 |
where, n =Orbit number, m =Mass number \[\left[ 9.1\times {{10}^{-31}}kg \right]\,,\]e =Charge on the electron \[\left[ 1.6\times {{10}^{-19}} \right]\] Z =Atomic number of element, k = Coulombic constant \[\left[ 9\times {{10}^{9}}N{{m}^{2}}{{c}^{-2}} \right]\]
After putting the values of m,e,k,h, we get.
\[{{r}_{n}}=\frac{{{n}^{2}}}{Z}\times 0.529{\AA}\ or\ {{r}_{n}}=\frac{{{n}^{2}}}{Z}\times 0.529nm\]
(a) For a particular system [e.g., H, He+ or Li+2]
\[r\propto {{n}^{2}}\][Z = constant]
Thus we have \[\frac{{{r}_{1}}}{{{r}_{2}}}=\frac{n_{1}^{2}}{n_{2}^{2}}\] i.e., \[{{r}_{1}}:{{r}_{2}}:{{r}_{3}}...........::1:4:9.......\]\[{{r}_{1}}<{{r}_{2}}<{{r}_{3}}\]
(b) For particular orbit of different species
\[r\propto \frac{1}{Z}\][Z =constant] Considering A and B species, we have \[\frac{{{r}_{A}}}{{{r}_{B}}}=\frac{{{Z}_{B}}}{{{Z}_{A}}}\]
Thus, radius of the first orbit H, \[H{{e}^{+}},L{{i}^{+2}}\]and \[B{{e}^{+3}}\]follows the order: \[H>H{{e}^{+}}>L{{i}^{+2}}>B{{e}^{+3}}\]
(iii) Calculation of velocity of electron
\[{{V}_{n}}=\frac{2\pi {{e}^{2}}ZK}{nh},\,{{V}_{n}}={{\left[ \frac{Z{{e}^{2}}}{mr} \right]}^{1/2}}\]
For H atom, \[{{V}_{n}}=\frac{2.188\times {{10}^{8}}}{n}cm.{{\sec }^{-1}}\]
(a) For a particular system [H, He+ or Li+2]
\[\text{V}\propto \frac{\text{1}}{\text{n}}\][Z = constant] Thus, we have, \[\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{{{n}_{2}}}{{{n}_{1}}}\]
The order of velocity is \[{{V}_{1}}>{{V}_{2}}>{{V}_{3}}.........\]or \[{{V}_{1}}:{{V}_{2}}:{{V}_{3}}..........::1:\frac{1}{2}:\frac{1}{3}........\]
(b) For a particular orbit of different species
\[V\propto Z\][n =constant] Thus, we have \[H<H{{e}^{+}}<L{{i}^{+2}}\]
(c) For H or He+ or Li+2, we have
\[{{V}_{1}}:{{V}_{2}}=2:1\,;\]\[{{V}_{1}}:{{V}_{3}}=3:1\,;\] \[{{V}_{1}}:{{V}_{4}}=4:1\]
(iv) Calculation of energy of electron in Bohr?s orbit
Total energy of electron = K.E. + P.E. of electron \[=\frac{kZ{{e}^{2}}}{2r}-\frac{kZ{{e}^{2}}}{r}=-\frac{kZ{{e}^{2}}}{2r}\]
Substituting of r, gives us \[E=\frac{-2{{\pi }^{2}}\,m{{Z}^{2}}{{e}^{4}}{{k}^{2}}}{{{n}^{2}}{{h}^{2}}}\] Where, n=1, 2, 3???.\[\infty \]
Putting the value of m, e, k, h,\[\pi \]we get
\[E=21.8\times {{10}^{-12}}\times \frac{{{Z}^{2}}}{{{n}^{2}}}erg\,per\,atom\]\[=-21.8\times {{10}^{-19}}\times \frac{{{Z}^{2}}}{{{n}^{2}}}J\,per\,atom\,(1J=\text{1}{{\text{0}}^{\text{7}}}erg)\]
\[E=-13.6\times \frac{{{Z}^{2}}}{{{n}^{2}}}eV\,per\,atom\text{(1eV}=\text{1}\text{.6}\times \text{1}{{\text{0}}^{-19}}J)=-313.6\times \frac{{{Z}^{2}}}{{{n}^{2}}}kcal./mole\] (1 cal = 4.18J)
or \[\frac{-1312}{{{n}^{2}}}{{Z}^{2}}kJmo{{l}^{-1}}\]
(a) For a particular system [H, He+ or Li+2]
\[E\propto -\frac{1}{{{n}^{2}}}\][Z =constant] Thus, we have \[\frac{{{E}_{1}}}{{{E}_{2}}}=\frac{n_{2}^{2}}{n_{1}^{2}}\]
The energy increase as the value of n increases
(b) For a particular orbit of different species
\[E\propto -{{Z}^{2}}\][n =constant] Thus, we have \[\frac{{{E}_{A}}}{{{E}_{B}}}=\frac{Z_{A}^{2}}{Z_{B}^{2}}\]
For the system H, He+, Li+2, Be+3 (n-same) the energy order is \[H>H{{e}^{+}}>L{{i}^{+2}}>B{{e}^{+3}}\]
The energy decreases as the value of atomic number Z increases.
When an electron jumps from an outer orbit (higher energy) \[{{n}_{2}}\]to an inner orbit (lower energy)\[{{n}_{1}},\]then the energy emitted in form of radiation is given by
\[\Delta E={{E}_{{{n}_{2}}}}-{{E}_{{{n}_{1}}}}=\frac{2{{\pi }^{2}}{{k}^{2}}m{{e}^{4}}{{Z}^{2}}}{{{h}^{2}}}\left( \frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}} \right)\,\Rightarrow \,\Delta E=13.6{{Z}^{2}}\left( \frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}} \right)\,eV/atom\]
As we know that \[E=h\bar{\nu },\]\[c=\nu \lambda \]and \[\bar{\nu }=\frac{1}{\lambda }\] \[=\frac{\Delta E}{hc},\] \[=\frac{2{{\pi }^{2}}{{k}^{2}}m{{e}^{4}}{{Z}^{2}}}{c{{h}^{3}}}\left( \frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}} \right)\]
This can be represented as\[\frac{1}{\lambda }=\bar{\nu }=R{{Z}^{2}}\left( \frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}} \right)\]where, \[R=\frac{2{{\pi }^{2}}{{k}^{2}}m{{e}^{4}}}{c{{h}^{3}}}R\]is known as Rydberg constant. Its value to be used is \[109678c{{m}^{-1}}.\]
(4) Quantisation of energy of electron
(i) In ground state : No energy emission. In ground state energy of atom is minimum and for 1st orbit of H-atom, n=1.
\[\therefore \,{{E}_{1}}=-13.6eV.\]
(ii) In excited state : Energy levels greater than \[{{n}_{1}}\] are excited state. i.e. for H- atom \[{{n}_{2}},\,{{n}_{3}},\,{{n}_{4}}\] are excited state. For H- atom first excitation state is \[={{n}_{2}}\]
(iii) Excitation potential : Energy required to excite electron from ground state to any excited state.
Ground state \[\xrightarrow{{}}\] Excited state
Ist excitation potential = \[{{E}_{2}}-{{E}_{1}}=-3.4+13.6=\]10.2 eV.
IInd excitation potential =\[{{E}_{3}}-{{E}_{1}}=-1.5+13.6=12.1\ eV.\]
(iv) Ionisation energy : The minimum energy required to relieve the electron from the binding of nucleus.
\[{{E}_{\text{ionisation}}}={{E}_{\infty }}-{{E}_{n}}=+13.6\frac{Z_{\text{eff}\text{.}}^{\text{2}}}{{{n}^{2}}}eV.\]
(v) Ionisation potential : \[{{V}_{\text{ionisation }}}=\frac{{{E}_{ionisation}}}{e}\]
(vi) Separation energy : Energy required to excite an electron from excited state to infinity.
S.E. = \[{{E}_{\infty }}-{{E}_{excited}}.\]
(vii) Binding energy : Energy released in bringing the electron from infinite to any orbit is called its binding energy (B.E.).
![]() Note : q Principal Quantum Number 'n' = \[\sqrt{\frac{13.6}{(B.E.)}}\].
Note : q Principal Quantum Number 'n' = \[\sqrt{\frac{13.6}{(B.E.)}}\].
(5) Spectral evidence for quantisation (Explanation for hydrogen spectrum on the basis of bohr atomic model)
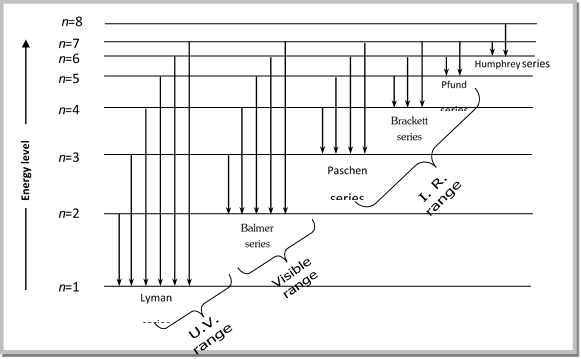
(i) The light absorbed or emitted as a result of an electron changing orbits produces characteristic absorption or emission spectra which can be recorded on the photographic plates as a series of lines, the optical spectrum of hydrogen consists of several series of lines called Lyman, Balmar, Paschen, Brackett, Pfund and Humphrey. These spectral series were named by the name of scientist who discovered them.
(ii) To evaluate wavelength of various H-lines Ritz introduced the following expression,
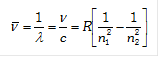
where, R is =\[\frac{2{{\pi }^{2}}m{{e}^{4}}}{c{{h}^{3}}}=\] Rydberg's constant
It's theoritical value = 109,737 cm–1 and It's experimental value = \[109,677.581c{{m}^{-1}}\]
This remarkable agreement between the theoretical and experimental value was great achievment of the Bohr model.
(iii) Although H- atom consists only one electron yet it's spectra consist of many spectral lines as shown in fig.
|
S.No. |
Spectral series |
Lies in the region |
Transition \[{{n}_{2}}>{{n}_{1}}\] |
\[{{\lambda }_{\text{max}}}=\frac{n_{1}^{2}n_{2}^{2}}{(n_{2}^{2}-n_{1}^{2})R}\] |
\[{{\lambda }_{\text{min}}}=\frac{n_{1}^{2}}{R}\] |
\[\frac{{{\lambda }_{\text{max}}}}{{{\lambda }_{\text{min}}}}=\frac{n_{2}^{2}}{n_{2}^{2}-n_{1}^{2}}\] |
|
(1) |
Lymen series |
Ultraviolet region |
\[{{n}_{1}}=1\] \[{{n}_{2}}=2,3,4....\infty \] |
\[{{n}_{1}}=1\text{ }\,\text{and }\,{{n}_{2}}=2\] \[{{\lambda }_{\text{max}}}=\frac{4}{3R}\] |
\[{{n}_{1}}=1\,\text{ and}\,{{n}_{2}}=\infty \] \[{{\lambda }_{\text{min}}}=\frac{1}{R}\] |
\[\frac{4}{3}\] |
|
(2) |
Balmer series |
Visible region |
\[{{n}_{1}}=2\] \[{{n}_{2}}=3,4,5....\infty \] |
\[{{n}_{1}}=2\,\text{ and }\,{{n}_{2}}=3\] \[{{\lambda }_{\text{max}}}=\frac{36}{5R}\] |
\[{{n}_{1}}=2\,\text{ and }\,{{n}_{2}}=\infty \] \[{{\lambda }_{\text{min}}}=\frac{4}{R}\] |
\[\frac{9}{5}\] |
|
(3) |
Paschen series |
Infra red region |
n1 = 3 \[{{n}_{2}}=4,5,6....\infty \] |
\[{{n}_{1}}=3\,\text{ and }\,{{n}_{2}}=4\] \[{{\lambda }_{\text{max}}}=\frac{144}{7R}\] |
\[{{n}_{1}}=3\,\text{ and}\,{{n}_{2}}=\infty \] \[{{\lambda }_{\text{min}}}=\frac{9}{R}\] |
\[\frac{16}{7}\] |
|
(4) |
Brackett series |
Infra red region |
\[{{n}_{1}}=4\] \[{{n}_{2}}=5,6,7....\infty \] |
\[{{n}_{1}}=4\,\text{ and }\,{{n}_{2}}=5\] \[{{\lambda }_{\text{max}}}=\frac{16\times 25}{9R}\] |
\[{{n}_{1}}=4\,\text{ and}\,{{n}_{2}}=\infty \] \[{{\lambda }_{\text{min}}}=\frac{16}{R}\] |
\[\frac{25}{9}\] |
|
(5) |
Pfund series |
Infra red region |
\[{{n}_{1}}=5\] \[{{n}_{2}}=6,7,8....\infty \] |
\[{{n}_{1}}=5\,\text{ and }\,{{n}_{2}}=6\] \[{{\lambda }_{\text{max}}}=\frac{25\times 36}{11R}\] |
\[{{n}_{1}}=5\,\text{ and}\,{{n}_{2}}=\infty \] \[{{\lambda }_{\text{min}}}=\frac{25}{R}\] |
\[\frac{36}{11}\] |
|
(6) |
Humphrey series |
Far infrared region |
\[{{n}_{1}}=6\] \[{{n}_{2}}=7,8....\infty \] |
\[{{n}_{1}}=6\,\text{ and }\,{{n}_{2}}=7\] \[{{\lambda }_{\text{max}}}=\frac{36\times 49}{13R}\] |
\[{{n}_{1}}=6\,\text{ and}\,{{n}_{2}}=\infty \] \[{{\lambda }_{\text{min}}}=\frac{36}{R}\] |
\[\frac{49}{13}\] |
(v) If an electron from nth excited state comes to various energy states, the maximum spectral lines obtained will be = \[\frac{n(n-1)}{2}.\] n= principal quantum number.
as n=6 than total number of spectral lines = \[\frac{6(6-1)}{2}=\frac{30}{2}=15.\]
(vi) Thus, at least for the hydrogen atom, the Bohr Theory accurately describes the origin of atomic spectral lines.
(6) Failure of Bohr Model
(i) Bohr Theory was very successful in predicting and accounting the energies of line spectra of hydrogen i.e. one electron system. It could not explain the line spectra of atoms containing more than one electron.
(ii) This theory could not explain the presence of multiple spectral lines.
(iii) This theory could not explain the splitting of spectral lines in magnetic field (Zeeman Effect) and in electric field (Stark effect). The intensity of these spectral lines was also not explained by the Bohr atomic model.
(iv) This theory was unable to explain of dual nature of matter as explained on the basis of De broglies concept.
(v) This theory could not explain uncertainty principle.
Example: 18 If the radius of 2nd Bohr orbit of hydrogen atom is r2. The radius of third Bohr orbit will be
(a) \[\frac{4}{9}{{r}_{2}}\] (b) \[4{{r}_{2}}\] (c) \[\frac{9}{4}{{r}_{3}}\] (d) \[9{{r}_{2}}\]
Solution : (c) \[r=\frac{{{n}^{2}}{{h}^{2}}}{4{{\pi }^{2}}mZ{{e}^{2}}}\] \[\therefore \] \[\frac{{{r}_{2}}}{{{r}_{3}}}=\frac{{{2}^{2}}}{{{3}^{2}}}\] \[\therefore \] \[{{r}_{3}}=\frac{9}{4}{{r}_{2}}\]
Example: 19 Number of waves made by a Bohr electron in one complete revolution in 3rd orbit is
(a) 2 (b) 3 (c) 4 (d) 1
Solution : (b) Circumference of 3rd orbit = \[2\pi {{r}_{3}}\]
According to Bohr angular momentum of electron in 3rd orbit is
mvr3 = \[3\frac{h}{2\pi }\] or \[\frac{h}{mv}=\frac{2\pi {{r}_{3}}}{3}\]
by De-Broglie equation, \[\lambda =\frac{h}{mv}\]
\[\therefore \,\lambda =\frac{2\pi {{r}_{3}}}{3}\] \[\therefore \,2\pi {{r}_{3}}=3\lambda \]
i.e. circumference of 3rd orbit is three times the wavelength of electron or number of waves made by Bohr electron in one complete revolution in 3rd orbit is three.
Example: 20 The degeneracy of the level of hydrogen atom that has energy \[-\frac{{{R}_{11}}}{16}\]is
(a) 16 (b) 4 (c) 2 (d) 1
Solution : (a) \[{{E}_{n}}=-\frac{{{R}_{H}}}{{{n}^{2}}}\] \[\therefore \] \[-\frac{{{R}_{H}}}{{{n}^{2}}}=-\frac{{{R}_{H}}}{16}\]
i.e. for \[{{4}^{th}}\] sub-shell
Example: 21 The velocity of electron in the ground state hydrogen atom is 2.18\[\times {{10}^{8}}m{{s}^{-1}}.\] Its velocity in the second orbit would be
(a) \[1.09\times {{10}^{8}}m{{s}^{-1}}\] (b) \[4.38\times {{10}^{8}}m{{s}^{-1}}\] (c) \[5.5\times {{10}^{5}}m{{s}^{-1}}\] (d) \[8.76\times {{10}^{8}}m{{s}^{-1}}\]
Solution : (a) We know that velocity of electron in nth Bohr's orbit is given by
\[v=2.18\times {{10}^{6}}\frac{Z}{n}m/s\]
for \[H,Z=1\]
\[\because \] \[{{v}_{1}}=\frac{2.18\times {{10}^{6}}}{1}m/s\]
\[\because \] \[{{v}_{2}}=\frac{2.18\times {{10}^{6}}}{2}m/s=1.09\times {{10}^{6}}m/s\]
Example: 22 The ionization energy of the ground state hydrogen atom is \[2.18\times {{10}^{-18}}J.\] The energy of an electron in its second orbit would be
(a) \[-\,1.09\times {{10}^{-18}}J\] (b) \[-2.18\times {{10}^{-18}}J\] (c) \[-4.36\times {{10}^{-18}}J\] (d) \[-5.45\times {{10}^{-19}}J\]
Solution : (d) Energy of electron in first Bohr's orbit of H-atom
\[E=\frac{-2.18\times {{10}^{-18}}}{{{n}^{2}}}J\] \[(\because \] ionization energy of H = \[2.18\times {{10}^{-18}}J\])
\[{{E}_{2}}=\frac{-2.18\times {{10}^{-18}}}{{{2}^{2}}}J=-5.45\times {{10}^{-19}}J\]
Example: 23 The wave number of first line of Balmer series of hydrogen atom is 15200\[c{{m}^{-1}}\]. What is the wave number of first line of Balmer series of \[L{{i}^{3+}}\] ion.
(a) \[15200c{{m}^{-1}}\] (b) 6080 \[c{{m}^{-1}}\] (c) \[76000c{{m}^{-1}}\] (d) \[1,36800\,c{{m}^{-1}}\]
Solution : (d) For \[L{{i}^{3+}}\ \bar{v}=\bar{v}\] for \[H\times {{z}^{2}}\] =15200 ×9= 1,36800\[c{{m}^{-1}}\]
Example: 24 The Bohr orbit radius for the hydrogen atom (n = 1) is approximately 0.530Å. The radius for the first excited state (n = 2) orbit is (in Å)
(a) 0.13 (b) 1.06 (c) 4.77 (d) 2.12
Solution : (d) The Bohr radius for hydrogen atom (n = 1) = 0.530Å
The radius of first excited state (n = 2) will be = \[0.530\times \frac{{{n}^{2}}}{Z}=0.530\times \frac{{{(2)}^{2}}}{1}=2.120{\AA}\]
Example: 25 How many chlorine atoms can you ionize in the process \[Cl\to C{{l}^{+}}+{{e}^{-}},\] by the energy liberated from the following process :
\[Cl+{{e}^{-}}\to C{{l}^{-}}\] for \[6\times {{10}^{23}}\] atoms
Given electron affinity of \[Cl=3.61eV,\] and \[IP\] of \[Cl=17.422\,eV\]
(a) 1.24\[\times {{10}^{23}}\] atoms (b) \[9.82\times {{10}^{20}}\] atoms (c) \[2.02\times {{10}^{15}}\] atoms (d) None of these
Solution : (a) Energy released in conversion of \[6\times {{10}^{23}}\] atoms of \[C{{l}^{-}}\] ions = \[6\times {{10}^{23}}\]× electron affinity
= 6×\[{{10}^{23}}\]\[\times 3.61=2.166\times {{10}^{24}}\]eV.
Let x Cl atoms are converted to \[C{{l}^{+}}\] ion
Energy absorbed \[=x\times \] ionization energy
\[x\times 17.422=2.166\times {{10}^{24}}\]; \[x=1.243\times {{10}^{23}}\] atoms
Example: 26 The binding energy of an electron in the ground state of the He atom is equal to 24eV. The energy required to remove both the electrons from the atom will be
(a) 59eV (b) 81eV (c) 79eV (d) None of these
Solution : (c) Ionization energy of He \[=\frac{{{Z}^{2}}}{{{n}^{2}}}\times 13.6\] \[=\frac{{{2}^{2}}}{{{1}^{2}}}\times 13.6\] \[=54.4eV\]
Energy required to remove both the electrons
\[=\] binding energy + ionization energy
\[=\] \[24.6+54.4\] \[=\] 79eV
Example: 27 The wave number of the shortest wavelength transition in Balmer series of atomic hydrogen will be
(a) 4215 Å (b) 1437Å (c) 3942Å (d) 3647Å
Solution : (d) \[\frac{1}{{{\lambda }_{\text{shortest}}}}=R{{Z}^{2}}\left( \frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}} \right)\] \[=\,109678\times {{1}^{2}}\times \left( \frac{1}{{{2}^{2}}}-\frac{1}{{{\infty }^{2}}} \right)\]
\[\lambda =3.647\times {{10}^{-5}}cm\] \[=\,3647{\AA}\]
Example: 28 If the speed of electron in the Bohr's first orbit of hydrogen atom is x, the speed of the electron in the third Bohr's orbit is
(a) x/9 (b) x/3 (c) 3x (d) 9x
Solution : (b) According to Bohr's model for hydrogen and hydrogen like atoms the velocity of an electron in an atom is quantised and is given by \[v\propto \frac{2\pi Z{{e}^{2}}}{nh}\] so \[v\propto \frac{1}{n}\] in this cass \[n=3\]
Example: 29 Of the following transitions in hydrogen atom, the one which gives an absorption line of lowest frequency is
(a) n=1 to n=2 (b) \[n=3\] to \[n=8\] (c) \[n=2\] to \[n=1\] (d) \[n=8\] to \[n=3\]
Solution : (b) Absorption line in the spectra arise when energy is absorbed i.e., electron shifts from lower to higher orbit, out of a & b, b will have the lowest frequency as this falls in the Paschen series.
Example: 30 The frequency of the line in the emission spectrum of hydrogen when the atoms of the gas contain electrons in the third energy level are
(a) \[1.268\times {{10}^{14}}Hz\] and \[2.864\times {{10}^{16}}Hz\] (b) \[3.214\times {{10}^{10}}Hz\] and \[1.124\times {{10}^{12}}Hz\]
(c) \[1.806\times {{10}^{12}}Hz\] and \[6.204\times {{10}^{15}}Hz\] (d) \[4.568\times {{10}^{14}}Hz\] and \[2.924\times {{10}^{15}}Hz\]
Solution : (d) If an electron is in 3rd orbit, two spectral lines are possible
(a) When it falls from 3rd orbit to 2nd orbit.
In equation \[\nu =3.289\times {{10}^{15}}\left[ \frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}} \right]\]
\[{{\nu }_{1}}=3.289\]\[\times {{10}^{15}}\left[ \frac{1}{{{2}^{2}}}-\frac{1}{{{3}^{2}}} \right]=3.289\times {{10}^{15}}\times \frac{5}{36}\]\[=\] \[4.568\times {{14}^{14}}Hz\]
(b) When it falls from 3rd orbit to 1st orbit :
\[{{\nu }_{2}}=3.289\times {{10}^{15}}\times \left[ \frac{1}{1}-\frac{1}{{{3}^{2}}} \right]=3.289\times {{10}^{15}}\times \frac{8}{9}=2.924\times {{10}^{15}}Hz\]
Example: 31 If the first ionisation energy of hydrogen is \[2.179\times {{10}^{-18}}J\] per atom, the second ionisation energy of helium per atom is
(a) \[8.716\times {{10}^{-18}}J\] (b) \[5.5250\,kJ\] (c) \[7.616\times {{10}^{-18}}J\] (d) \[8.016\times {{10}^{-13}}J\]
Solution : (a) For Bohrs systems : energy of the electron \[\propto \frac{{{Z}^{2}}}{{{n}^{2}}}\]
Ionisation energy is the difference of energies of an electron \[({{E}_{\infty }}),\] when taken to infinite distance and \[{{E}_{r}}\] when present in any Bohr orbit and \[{{E}_{\alpha }}\] is taken as zero so ionisation energy becomes equal to the energy of electron in any Bohr orbit.
\[{{E}_{H}}\propto \frac{Z_{H}^{2}}{n_{H}^{2}}\] ; \[{{E}_{He}}\,\,\propto \,\frac{Z_{He}^{2}}{n_{He}^{2}}\] or \[\frac{{{E}_{H}}}{{{E}_{He}}}=\frac{1}{2\times 2}\] [as \[{{Z}_{H}}=1,\,\,{{Z}_{He}}=2,\,{{n}_{H}}=1,\,{{n}_{He}}=1]\]
or\[{{E}_{He}}={{E}_{H}}\times 4=2.179\times {{10}^{-18}}\times 4=8.716\times {{10}^{-18}}\] Joule per atom.
Example: 32 The ionization energy of hydrogen atom is 13.6eV. What will be the ionization energy of \[H{{e}^{+}}\]
(a) 13.6eV (b) 54.4eV (c) 122.4eV (d) Zero
Solution : (b) I.E. of \[H{{e}^{+}}=13.6eV\times {{Z}^{2}}\]
\[13.6eV\times 4=54.4eV\]
Example: 33 The ionization energy of \[H{{e}^{+}}\] is \[19.6\times {{10}^{-18}}\]J atom–1. Calculate the energy of the first stationary state of \[L{{i}^{+2}}\]
(a) \[19.6\times {{10}^{-18}}J\,\text{ato}{{\text{m}}^{\text{-1}}}\] (b) \[4.41\times {{10}^{-18}}J\] atom–1
(c) \[19.6\times {{10}^{-19}}J\,\text{ato}{{\text{m}}^{\text{-1}}}\] (d) \[4.41\times {{10}^{-17}}J\,\text{ato}{{\text{m}}^{-\text{1}}}\]
Solution : (d) I.E. of \[H{{e}^{+}}=E\times {{2}^{2}}(Z\] for \[He=2)\]
I.E. of \[L{{i}^{2+}}=E\times {{3}^{3}}\](Z for Li=3)
\[\therefore \frac{I.E.(H{{e}^{+}})}{I.E.(L{{i}^{2+}})}=\frac{4}{9}\] or I.E. \[(L{{i}^{2+}})=\frac{9}{4}\times I.E.(H{{e}^{+}})\] \[=\frac{9}{4}\times 19.6\times {{10}^{-18}}\] =\[4.41\times {{10}^{-17}}\] J atom–1
Bohr – Sommerfeld’s model.
(1) In 1915, Sommerfield introduced a new atomic model to explain the fine spectrum of hydrogen atom.
(2) He gave concept that electron revolve round the nucleus in elliptical orbit. Circular orbits are formed in special conditions only when major axis and minor axis of orbit are equal.
(3) For circular orbit, the angular momentum = \[\frac{nh}{2\pi }\] where n= principal quantum number only one component i.e. only angle changes.
(4) For elliptical orbit, angular momentum = vector sum of 2 components. In elliptical orbit two components are,
(i) Radial component (along the radius) = \[{{n}_{r}}\,\frac{h}{2\pi }\]
Where, n\[{}_{r}\]= radial quantum number
(ii) Azimuthal component = n\[_{\varphi }\]\[\frac{h}{2\pi }\]
Where, n\[{}_{\varphi }\]= azimuthal quantum number
So angular momentum of elliptical orbit =\[n{}_{r}\frac{h}{2\pi }\,+\,n{}_{\varphi }\frac{h}{2\pi }\]
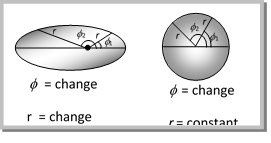
Angular momentum = \[(n{}_{r}+\,\,n{}_{\varphi })\,\frac{h}{2\pi }\]
(5) Shape of elliptical orbit depends on,
\[\frac{\text{Length}\,\text{of}\,\text{major}\,\text{axis}}{\text{Length}\,\text{of}\,\text{minor}\,\text{axis}}=\,\frac{n}{{{n}_{\varphi }}}\]\[=\frac{{{n}_{r}}+{{n}_{\varphi }}}{{{n}_{\varphi }}}\]
(6) n\[{}_{\varphi }\] can take all integral values from l to ‘n’ values of n\[{}_{r}\] depend on the value of n\[{}_{\varphi }\]. For n = 3, n\[{}_{\varphi }\]can have values 1,2,3 and n\[{}_{r}\] can have (n –1) to zero i.e. 2,1 and zero respectively.
Thus for n = 3, we have 3 paths
n n\[{}_{\varphi }\] n\[{}_{r}\] Nature of path
3 1 3 elliptical
2 1 elliptical
3 0 circular
The possible orbits for n = 3 are shown in figure.
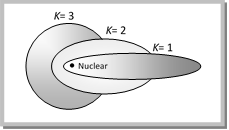
Thus Sommerfield showed that Bohr’s each major level was composed of several sub-levels therefore it provides the basis for existance of subshells in Bohr's shells (orbits).
(7) Limitation of Bohr sommerfield model :
(i) This model could not account for, why electrons does not absorb or emit energy when they are moving in stationary orbits.
(ii) When electron jumps from inner orbit to outer orbit or vice –versa, then electron run entire distance but absorption or emission of energy is discontinuous.
(iii) It could not explain the attainment of expression of \[\frac{nh}{2\pi }\] for angular momentum. This model could not explain Zeeman effect and Stark effect.
You need to login to perform this action.
You will be redirected in
3 sec
