Acceleration
Category : NEET
Acceleration
The time rate of change of velocity of an object is called acceleration of the object.
(1) It is a vector quantity. It’s direction is same as that of change in velocity (Not of the velocity)
(2) There are three possible ways by which change in velocity may occur
|
When only direction of velocity changes |
When only magnitude of velocity changes |
When both magnitude and direction of velocity changes |
|
Acceleration perpendicular to velocity |
Acceleration parallel or anti-parallel to velocity |
Acceleration has two components one is perpendicular to velocity and another parallel or anti-parallel to velocity |
|
e.g. Uniform circular motion |
e.g. Motion under gravity |
e.g. Projectile motion |
(3) Dimension: \[\left[ {{M}^{0}}{{L}^{1}}{{T}^{2}} \right]\]
(4) Unit: metre/second2 (S.I.); cm/second2 (C.G.S.)
(5) Types of acceleration:
(i) Uniform acceleration: A body is said to have uniform acceleration if magnitude and direction of the acceleration remains constant during particle motion.
Note: q If a particle is moving with uniform acceleration, this does not necessarily imply that particle is moving in straight line. e.g. Projectile motion.
(ii) Non-uniform acceleration: A body is said to have non-uniform acceleration, if magnitude or direction or both, change during motion.
(iii) Average acceleration: \[{{\vec{a}}_{a\upsilon }}=\frac{\Delta \vec{v}}{\Delta \vec{t}}=\frac{{{{\vec{v}}}_{2}}-{{{\vec{v}}}_{1}}}{\Delta t}\]
The direction of average acceleration vector is the direction of the change in velocity vector as \[\vec{a}=\frac{\Delta \vec{v}}{\Delta t}\]
(iv) Instantaneous acceleration \[=\,\,\vec{a}=\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{\Delta \vec{v}}{\Delta t}=\frac{d\vec{v}}{dt}\]
(v) For a moving body there is no relation between the direction of instantaneous velocity and direction of acceleration.

e.g. (a) In uniform circular motion \[\theta =90{}^\text{o}\] always
(b) In a projectile motion \[\theta \] is variable for every point of trajectory.
(vi) If a force \[\overrightarrow{F}\] acts on a particle of mass m, by Newton’s 2nd law, acceleration \[\vec{a}=\frac{{\vec{F}}}{m}\]
(vii) By definition \[\vec{a}=\frac{d\vec{v}}{dt}=\frac{{{d}^{2}}\vec{x}}{d{{t}^{2}}}\left[ \text{As}\,\,\vec{v}=\frac{d\vec{x}}{dt} \right]\]
i.e., if x is given as a function of time, second time derivative of displacement gives acceleration
(viii) If velocity is given as a function of position, then by chain rule \[a=\frac{dv}{dt}=\frac{dv}{dx}\times \frac{dx}{dt}=v.\frac{d\upsilon }{dx}\,\left[ \text{as}\,\,v=\frac{dx}{dt} \right]\]
(ix) If a particle is accelerated for a time t1 by acceleration a1 and for time t2 by acceleration a2 then average acceleration is \[{{a}_{a\upsilon }}=\frac{{{a}_{1}}{{t}_{1}}+{{a}_{2}}{{t}_{2}}}{{{t}_{1}}+{{t}_{2}}}\]
(x) If same force is applied on two bodies of different masses \[{{m}_{1}}\] and \[{{m}_{2}}\] separately then it produces accelerations \[{{a}_{1}}\,\,and\,\,{{a}_{2}}\] respectively. Now these bodies are attached together and form a combined system and same force is applied on that system so that a be the acceleration of the combined system, then
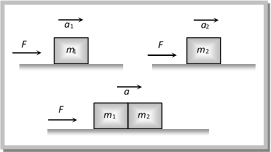
\[F=\left( {{m}_{1}}+{{m}_{2}} \right)\,a\,\,\,\Rightarrow \,\,\,\frac{F}{a}=\frac{F}{{{a}_{1}}}+\frac{F}{{{a}_{2}}}\]
So, \[\frac{1}{a}=\frac{1}{{{a}_{1}}}+\frac{1}{{{a}_{2}}}\Rightarrow a=\frac{{{a}_{1}}{{a}_{2}}}{{{a}_{1}}+{{a}_{2}}}\]
(xi) Acceleration can be positive, zero or negative. Positive acceleration means velocity increasing with time, zero acceleration means velocity is uniform constant while negative acceleration (retardation) means velocity is decreasing with time.
(xii) For motion of a body under gravity, acceleration will be equal to “g”, where g is the acceleration due to gravity. Its normal value is \[9.8\,\,\text{m/}{{\text{s}}^{\text{2}}}\] or \[980\,\,\text{cm/}{{\text{s}}^{\text{2}}}\] or \[32\,\,\text{feet/}{{\text{s}}^{\text{2}}}\].
Sample problems based on acceleration
Problem 12. The displacement of a particle, moving in a straight line, is given by \[s=2{{t}^{2}}+2t+4\] where \[s\] is in metres and \[t\] in seconds. The acceleration of the particle is [CPMT 2001]
(a) \[2\text{ }m/{{s}^{2}}\] (b) \[4 m/{{s}^{2}}\] (c) \[6 m/{{s}^{2}}\] (d) \[8 m/{{s}^{2}}\]
Solution: (b) Given \[s=2{{t}^{2}}+2t+4\] \ velocity (v) \[=\frac{ds}{dt}=4t+2\] and acceleration (a) \[=\frac{dv}{dt}=4(1)+0=4m/{{s}^{2}}\]
Problem 13. The position x of a particle varies with time t as \[x=a{{t}^{2}}-b{{t}^{3}}.\] The acceleration of the particle will be zero at time t equal to [CBSE PMT 1997; BHU 1999; DPMT 2000; KCET (Med.) 2000]
(a) \[\frac{a}{b}\] (b) \[\frac{2a}{3b}\] (c) \[\frac{a}{3b}\] (d) Zero
Solution: (c) Given \[x=a{{t}^{2}}-b{{t}^{3}}\] \ velocity \[(v)=\frac{dx}{dt}=2at-3b{{t}^{2}}\] and acceleration (a) \[=\frac{dv}{dt}=2a-6bt.\]
When acceleration \[=\,\,0\Rightarrow 2a-6bt=0\Rightarrow \,t=\frac{2a}{6b}=\frac{a}{3b}\]
Problem 14. The displacement of the particle is given by \[y=a+bt+c{{t}^{2}}-d{{t}^{4}}.\] The initial velocity and acceleration are respectively [CPMT 1999, 2003]
(a) \[b,\,\,-\,4d\] (b) \[-b,\,2c\] (c) \[b,\,2c\] (d) \[2c,\,-4d\]
Solution: (c) Given \[y=a+bt+c{{t}^{2}}-d{{t}^{4}}\] \[\therefore \,\,\,\,v=\frac{dy}{dt}=0+b+2ct-4d{{t}^{3}}\]
Putting \[t=0,\,\,{{v}_{initial}}=\text{ }b\]
So initial velocity = b
Now, acceleration (a) \[=\frac{dv}{dt}=0+2c-12\,d\,{{t}^{2}}\]
Putting \[\operatorname{t} = 0, \,{{a}_{initial}}= 2c\]
Problem 15. The relation between time t and distance x is \[t=\alpha \,{{x}^{2}}+\beta x,\] where a and b are constants. The retardation is (v is the velocity) [NCERT 1982]
(a) \[2\alpha {{v}^{3}}\] (b) \[2\beta {{v}^{3}}\] (c) \[2\alpha \beta {{v}^{3}}\] (d) \[2{{\beta }^{2}}{{v}^{3}}\]
Solution: (a) differentiating time with respect to distance \[\frac{dt}{dx}=2\alpha x+\beta \Rightarrow v=\frac{dx}{dt}=\frac{1}{2\alpha x+\beta }\]
So, acceleration (a) \[=\frac{dv}{dt}=\frac{dv}{dx}.\frac{dx}{dt}=v\frac{dv}{dx}=\frac{-v.\,2\alpha }{{{(2\alpha x+\beta )}^{2}}}=-2\alpha .v.{{v}^{2}}=-2\alpha {{v}^{3}}\]
Problem 16. If displacement of a particle is directly proportional to the square of time. Then particle is moving with
[RPET 1999]
(a) Uniform acceleration (b) Variable acceleration
(c) Uniform velocity (d) Variable acceleration but uniform velocity
Solution: (a) Given that \[x\,\propto \,{{t}^{2}}\,\,or\,\,x\,=\,K{{t}^{2}}\] (where K = constant)
Velocity (v) \[=\frac{dx}{dt}=2Kt\] and Acceleration (a) \[=\frac{d\upsilon }{dt}=2K\]
It is clear that velocity is time dependent and acceleration does not depend on time.
So we can say that particle is moving with uniform acceleration but variable velocity.
Problem 17. A particle is moving eastwards with velocity of 5 m/s. In 10 sec the velocity changes to 5 m/s northwards. The average acceleration in this time is [IIT-JEE 1982]
(a) Zero (b) \[\frac{1}{\sqrt{2}}\,\,\text{m/}{{\text{s}}^{\text{2}}}\] toward north-west
(c) \[\frac{1}{\sqrt{2}}\,\,\text{m/}{{\text{s}}^{\text{2}}}\] toward north-east (d) \[\frac{1}{2}\,\,\text{m/}{{\text{s}}^{\text{2}}}\] toward north-west
Solution: (b) \[\Delta \vec{\upsilon }={{\vec{\upsilon }}_{2}}-{{\vec{\upsilon }}_{1}}\]
\[\Delta \upsilon =\sqrt{\upsilon _{1}^{2}+\upsilon _{2}^{2}-2{{\upsilon }_{1}}{{\upsilon }_{2}}\,\,\cos {{90}^{o}}}=\sqrt{{{5}^{2}}+{{5}^{2}}}=5\sqrt{2}\] 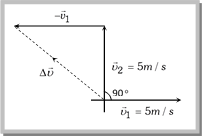
\[\Delta \upsilon =5\sqrt{2}\]
Average acceleration \[=\frac{\Delta \upsilon }{\Delta t}=\frac{5\sqrt{2}}{10}=\frac{1}{\sqrt{2}}\,\,\text{m/}{{\text{s}}^{\text{2}}}\] toward north-west (As clear from the figure).
Problem 18. A body starts from the origin and moves along the x-axis such that velocity at any instant is given by \[(4{{t}^{3}}-2t)\], where t is in second and velocity is in m/s. What is the acceleration of the particle, when it is 2m from the origin? [IIT-JEE 1982]
(a) \[28\,\,m/{{s}^{\text{2}}}\] (b) \[22\,\,m/{{s}^{\text{2}}}\] (c) \[12\,\,m\text{/}{{s}^{\text{2}}}\] (d) \[10\,\,m\text{/}{{s}^{\text{2}}}\]
Solution: (b) Given that \[\upsilon =4{{t}^{3}}-2t\]
\[x=\int{\upsilon \,dt}\], \[x={{t}^{4}}-{{t}^{2}}+C\], at \[t=0,\,x=0\,\,\,\Rightarrow \,C=0\]
When particle is 2m away from the origin
\[2={{t}^{4}}-{{t}^{2}}\Rightarrow {{t}^{4}}-{{t}^{2}}-2=0\Rightarrow ({{t}^{2}}-2)\,\,({{t}^{2}}+1)=0\Rightarrow t=\sqrt{2}\,\sec \]
\[a=\frac{d\upsilon }{d\,t}=\frac{d}{d\,t}\left( 4{{t}^{3}}-2t \right)=12{{t}^{2}}-2\Rightarrow a=12{{t}^{2}}-2\]
for \[t=\sqrt{2}\sec \Rightarrow a=12\times {{\left( \sqrt{2} \right)}^{2}}-2\Rightarrow a=22\,\,m\text{/}{{s}^{\text{2}}}\]
You need to login to perform this action.
You will be redirected in
3 sec
