Motion Under Gravity
Category : NEET
Motion Under Gravity
The force of attraction of earth on bodies, is called force of gravity. Acceleration produced in the body by the force of gravity, is called acceleration due to gravity. It is represented by the symbol g.
In the absence of air resistance, it is found that all bodies (irrespective of the size, weight or composition) fall with the same acceleration near the surface of the earth. This motion of a body falling towards the earth from a small altitude \[\left( h << R \right)\] is called free fall.
An ideal one-dimensional motion under gravity in which air resistance and the small changes in acceleration with height are neglected.
(1) If a body dropped from some height (initial velocity zero)
(i) Equation of motion: Taking initial position as origin and direction of motion (i.e., downward direction) as a positive, here we have 
u = 0 [As body starts from rest]
a = +g [As acceleration is in the direction of motion]
v = g t … (i)
\[h=\frac{1}{2}g{{t}^{2}}\] … (ii)
\[{{\upsilon }^{2}}=2gh\] … (iii)
\[{{h}_{n}}=\frac{g}{2}(2n-1)\] ... (iv)
(ii) Graph of distance velocity and acceleration with respect to time: time:

(iii) As \[\operatorname{h} = \left( 1/2 \right)\,g{{t}^{2}}, i.e., h\propto {{t}^{2}}\], distance covered in time t, 2t, 3t, etc., will be in the ratio of \[{{1}^{2}}:\text{ }{{2}^{2}}:\text{ }{{3}^{2}}\], i.e., square of integers.
(iv) The distance covered in the nth sec, \[{{h}_{n}}=\frac{1}{2}g\,(2n-1)\]
So distance covered in I, II, III sec, etc., will be in the ratio of \[1 : 3 : 5\], i.e., odd integers only.
(2) If a body is projected vertically downward with some initial velocity
Equation of motion: \[\upsilon =u+g\,t\]
\[h=ut+\frac{1}{2}g\,{{t}^{2}}\]
\[{{\upsilon }^{2}}={{u}^{2}}+2gh\]
\[{{h}_{n}}=u+\frac{g}{2}\,(2n-1)\]
(3) If a body is projected vertically upward
(i) Equation of motion: Taking initial position as origin and direction of motion (i.e., vertically up) as positive
\[\operatorname{a} = g\] [As acceleration is downwards while motion upwards]
So, if the body is projected with velocity u and after time t it reaches up to height h then

\[\upsilon =u-g\,t\]; \[h=ut-\frac{1}{2}g\,{{t}^{2}}\]; \[{{\upsilon }^{2}}={{u}^{2}}-2gh;\,\,{{h}_{n}}=u-\frac{g}{2}\,(2n-1)\]
(ii) For maximum height \[\operatorname{v} = 0\]
So from above equation
\[\operatorname{u} = gt,\]
\[h=\frac{1}{2}g{{t}^{2}}\]
and \[{{u}^{2}}=2gh\]
(iii) Graph of distance, velocity and acceleration with respect to time (for maximum height):

It is clear that both quantities do not depend upon the mass of the body or we can say that in absence of air resistance, all bodies fall on the surface of the earth with the same rate.
(4) In case of motion under gravity for a given body, mass, acceleration, and mechanical energy remain constant while speed, velocity, momentum, kinetic energy and potential energy change.
(5) The motion is independent of the mass of the body, as in any equation of motion, mass is not involved. That is why a heavy and light body when released from the same height, reach the ground simultaneously and with same velocity i.e., \[t=\sqrt{(2h/g)}\] and \[v=\sqrt{2gh}\].
(6) In case of motion under gravity time taken to go up is equal to the time taken to fall down through the same distance. Time of descent (t1) = time of ascent \[\left( {{t}_{2}} \right) = u/g\]
\[\therefore \] Total time of flight \[T\text{ }=\text{ }{{t}_{1}}+\text{ }{{t}_{2}}=\frac{2u}{g}\]
(7) In case of motion under gravity, the speed with which a body is projected up is equal to the speed with which it comes back to the point of projection.
As well as the magnitude of velocity at any point on the path is same whether the body is moving in upwards or downward direction.
(8) A ball is dropped from a building of height h and it reaches after t seconds on earth. From the same building if two ball are thrown (one upwards and other downwards) with the same velocity u and they reach the earth surface after t1 and t2 seconds respectively then
\[t=\sqrt{{{t}_{1}}{{t}_{2}}}\]

(9) A body is thrown vertically upwards. If air resistance is to be taken into account, then the time of ascent is less than the time of descent. \[{{\operatorname{t}}_{2}}> {{t}_{1}}\]
Let u is the initial velocity of body then time of ascent \[{{t}_{1}}=\frac{u}{g+a}\] and \[h=\frac{{{u}^{2}}}{2(g+a)}\]
where g is acceleration due to gravity and a is retardation by air resistance and for upward motion both will work vertically downward.
For downward motion a and g will work in opposite direction because a always work in direction opposite to motion and g always work vertically downward.
So \[h=\frac{1}{2}(g-a)\,t_{2}^{2}\Rightarrow \frac{{{u}^{2}}}{2(g+a)}=\frac{1}{2}(g-a)\,t_{2}^{2}\Rightarrow {{t}_{2}}=\frac{u}{\sqrt{(g+a)(g-a)}}\]
Comparing t1 and t2 we can say that \[{{\operatorname{t}}_{2}}> {{t}_{1}}\] since \[\left( g + a \right) > \left( g a \right)\]
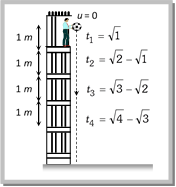
(10) A particle is dropped vertically from rest from a height. The time taken by it to fall through successive distance of 1m each will then be in the ratio of the difference in the square roots of the integers i.e.
\[\sqrt{1},(\sqrt{2}-\sqrt{1}),\,(\sqrt{3}-\sqrt{2}).......(\sqrt{4}-\sqrt{3}),.........\]
Sample problems based on motion under gravity
Problem 51. If a body is thrown up with the velocity of 15 m/s then maximum height attained by the body is (g = 10 m/s2) [MP PMT 2003]
(a) 11.25 m (b) 16.2 m (c) 24.5 m (d) 7.62 m
Solution: (a) \[{{H}_{\max }}=\frac{{{u}^{2}}}{2g}=\frac{{{(15)}^{2}}}{2\times 10}=11.25m\]
Problem 52. A body falls from rest in the gravitational field of the earth. The distance travelled in the fifth second of its motion is \[(g=10m/{{s}^{2}})\] [MP PET 2003]
(a) 25 m (b) 45 m (c) 90 m (d) 125 m
Solution: (b) \[{{h}_{n}}=\frac{g}{2}\left( 2n-1 \right)\,\Rightarrow \,{{h}_{5th}}=\frac{10}{2}\left( 2\times 5-1 \right)=45\,m.\]
Problem 53. If a ball is thrown vertically upwards with speed u, the distance covered during the last t seconds of its ascent is [CBSE 2003]
(a) \[\frac{1}{2}g{{t}^{2}}\] (b) \[ut-\frac{1}{2}g{{t}^{2}}\] (c) \[(u-gt)t\] (d) \[ut\]
Solution: (a) If ball is thrown with velocity u, then time of flight \[=\frac{u}{g}\]
velocity after \[\left( \frac{u}{g}-t \right)\,\sec \,:v=u-g\left( \frac{u}{g}-t \right)=\text{ }gt\]
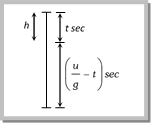
So, distance in last 't' sec: \[{{0}^{2}}={{(gt)}^{2}}-2(g)h.\]
\[\Rightarrow h=\frac{1}{2}g{{t}^{2}}.\]
Problem 54. A man throws balls with the same speed vertically upwards one after the other at an interval of 2 seconds. What should be the speed of the throw so that more than two balls are in the sky at any time (Given \[g=9.8m/{{s}^{2}})\] [CBSE PMT 2003]
(a) At least 0.8 m/s (b) Any speed less than 19.6 m/s
(c) Only with speed 19.6 m/s (d) More than 19.6 m/s
Solution: (d) Interval of ball throw = 2 sec.
If we want that minimum three (more than two) ball remain in air then time of flight of first ball must be greater than 4 sec. i.e. \[T\,>4\,sec\] or \[\frac{2U}{g}\,>\,4\,sec\,\Rightarrow \,u>19.6\,m/s\]
It is clear that for \[u\,=\,19.6\] First ball will just strike the ground (in sky), second ball will be at highest point (in sky), and third ball will be at point of projection or on ground (not in sky).
Problem 55. A man drops a ball downside from the roof of a tower of height 400 meters. At the same time another ball is thrown upside with a velocity 50 meter/sec. from the surface of the tower, then they will meet at which height from the surface of the tower [CPMT 2003]
(a) 100 meters (b) 320 meters (c) 80 meters (d) 240 meters
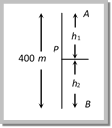
Solution: (c) Let both balls meet at point P after time t.
The distance travelled by ball A \[({{h}_{1}})=\frac{1}{2}g{{t}^{2}}\] ..... (i)
The distance travelled by ball B \[({{h}_{2}})\,=\,ut-\,\frac{1}{2}g{{t}^{2}}\] ..... (ii)
By adding (i) and (ii) \[{{h}_{1}}+{{h}_{2}}\,=\,ut\,=\text{ }400\] (Given \[h={{h}_{1}}+{{h}_{2}}=400.\])
\[\therefore \,\,\,\,t=\,400/50\,=\,8sec\] and \[{{h}_{1}}=\,320\,m\text{, }\,{{h}_{2}}=\,80\,m\]
Problem 56. A very large number of balls are thrown vertically upwards in quick succession in such a way that the next ball is thrown when the previous one is at the maximum height. If the maximum height is 5m, the number of ball thrown per minute is (take \[g=10\,m{{s}^{-2}}\]) [KCET (Med.) 2002]
(a) 120 (b) 80 (c) 60 (d) 40
Solution: (c) Maximum height of ball = 5m, So velocity of projection \[\Rightarrow u=\sqrt{2gh}=\sqrt{2\times 10\times 5}\,=\,10\,m/s\] time interval between two balls (time of ascent) \[=\frac{u}{g}\,=\,1sec=\frac{1}{60}min.\]
So no. of ball thrown per min = 60
Problem 57. A particle is thrown vertically upwards. If its velocity at half of the maximum height is 10 m/s, then maximum height attained by it is (Take \[g=10\,m/{{s}^{2}}\]) [CBSE PMT 2001]
(a) 8 m (b) 10 m (c) 12 m (d) 16 m
Solution: (b) Let particle thrown with velocity u and its maximum height is \[H\] then \[H=\frac{{{u}^{2}}}{2g}\]
When particle is at a height \[H/2\], then its speed is \[10\,m/s\]
From equation \[{{v}^{2}}={{u}^{2}}-2gh\], \[{{\left( 10 \right)}^{2}}={{u}^{2}}-2g\,\left( \frac{H}{2} \right)=\,{{u}^{2}}-2g\,\frac{{{u}^{2}}}{4g}\Rightarrow \,{{u}^{2}}=200\]
\[\therefore \] Maximum height \[\,H=\frac{{{u}^{2}}}{2g}=\frac{200}{2\times 10}=\text{ }10\,m\]
Problem 58. A stone is shot straight upward with a speed of 20 m/sec from a tower 200 m high. The speed with which it strikes the ground is approximately [AMU (Engg.) 1999]
(a) 60 m/sec (b) 65 m/sec (c) 70 m/sec (d) 75 m/sec
Solution: (b) Speed of stone in a vertically upward direction is 20 m/s. So for vertical downward motion we will consider \[u=-20\,m/s\]
\[{{v}^{2}}={{u}^{2}}+2gh={{(-20)}^{2}}+2\times 10\times 200\,\,\Rightarrow \,v=65\,\,m/s\]
Problem 59. A body freely falling from the rest has a velocity ‘v’ after it falls through a height ‘h’. The distance it has to fall down for its velocity to become double, is [BHU 1999]
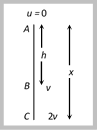
(a) \[2h\] (b) \[4h\] (c) \[6h\] (d) \[8h\]
Solution: (b) Let at point A initial velocity of body is equal to zero
For path AB: \[{{v}^{2}}=0+2gh\,\] … (i)
For path AC: \[{{(2v)}^{2}}=0+2gx\]Þ \[4{{v}^{2}}=2gx\] … (ii)
Solving (i) and (ii) \[x=4h\]
Problem 60. A body sliding on a smooth inclined plane requires 4 seconds to reach the bottom starting from rest at the top. How much time does it take to cover one-fourth distance starting from rest at the top [BHU 1998]
(a) 1 s (b) 2 s (c) 4 s (d) 16 s
Solution: (b) \[S=\frac{1}{2}a{{t}^{2}}\Rightarrow t\propto \sqrt{s}\] \[\left( As\,\text{a}=\text{ constant} \right)\]
\[\frac{{{t}_{2}}}{{{t}_{1}}}=\sqrt{\frac{{{s}_{2}}}{{{s}_{1}}}}=\sqrt{\frac{s/4}{s}}=\frac{1}{2}\Rightarrow \] \[{{t}_{2}}=\frac{{{t}_{1}}}{2}=\frac{4}{2}=2\,s\]
Problem 61. A stone dropped from a building of height h and it reaches after t seconds on earth. From the same building if two stones are thrown (one upwards and other downwards) with the same velocity u and they reach the earth surface after \[{{t}_{1}}\]and \[{{t}_{2}}\] seconds respectively, then [CPMT 1997; UPSEAT 2002; KCET (Engg./Med.) 2002]
(a) \[t={{t}_{1}}-{{t}_{2}}\] (b) \[t=\frac{{{t}_{1}}+{{t}_{2}}}{2}\] (c) \[t=\sqrt{{{t}_{1}}{{t}_{2}}}\] (d) \[t=t_{1}^{2}\,t_{2}^{2}\]
Solution: (c) For first case of dropping \[h=\frac{1}{2}g{{t}^{2}}.\]
For second case of downward throwing \[h=-u{{t}_{1}}+\frac{1}{2}gt_{1}^{2}=\frac{1}{2}g{{t}^{2}}\]
\[\Rightarrow -u{{t}_{1}}=\frac{1}{2}g({{t}^{2}}-t_{1}^{2})\] ...... (i)
For third case of upward throwing \[h=u{{t}_{2}}+\frac{1}{2}gt_{2}^{2}=\frac{1}{2}g{{t}^{2}}\]
Þ \[u{{t}_{2}}=\frac{1}{2}g({{t}^{2}}-t_{2}^{2})\] ....... (ii)
on solving these two equations : \[-\frac{{{t}_{1}}}{{{t}_{2}}}=\frac{{{t}^{2}}-t_{1}^{2}}{{{t}^{2}}-t_{2}^{2}}\Rightarrow t=\sqrt{{{t}_{1}}{{t}_{2}}.}\]
Problem 62. By which velocity a ball be projected vertically downward so that the distance covered by it in 5th second is twice the distance it covers in its 6th second (\[g=10\,m/{{s}^{2}}\]) [CPMT 1997; MH CET 2000]
(a) \[58.8\,m/s\] (b) \[49\,m/s\]
(c) \[65\,m/s\] (d) \[19.6\,m/s\]
Solution: (c) By formula \[{{h}_{n}}=u+\frac{1}{2}g\,(2n-1)\Rightarrow u-\frac{10}{2}[2\times 5-1]=2\,\{u-\frac{10}{2}[2\times 6-1]\}\]
\[\Rightarrow \,\,\,u-45=2\times (u-55)\Rightarrow u=65m/s.\]
Problem 63. Water drops fall at regular intervals from a tap which is 5 m above the ground. The third drop is leaving the tap at the instant the first drop touches the ground. How far above the ground is the second drop at that instant [CBSE PMT 1995]
(a) 2.50 m (b) 3.75 m
(c) 4.00 m (d) 1.25 m
Solution: (b) Let the interval be t then from question
For first drop \[\frac{1}{2}g{{(2t)}^{2}}=5\] ..... (i) For second drop \[x=\frac{1}{2}g{{t}^{2}}\] .....(ii)
By solving (i) and (ii) \[x=\frac{5}{4}\] and hence required height \[h=5-\frac{5}{4}=3.75\,m.\]
Problem 64. A balloon is at a height of 81 m and is ascending upwards with a velocity of \[12\,m/s.\]A body of 2 kg weight is dropped from it. If \[g=10\,m/{{s}^{2}},\] the body will reach the surface of the earth in [MP PMT 1994]
(a) 1.5 s (b) 4.025 s (c) 5.4 s (d) 6.75 s
Solution: (c) As the balloon is going up we will take initial velocity of falling body \[=-12m/s,\] \[h=81m,\,\] \[g=+10m/{{s}^{2}}\]
By applying \[h=ut+\frac{1}{2}g{{t}^{2}}\]; \[\,81=-12t+\frac{1}{2}(10){{t}^{2}}\Rightarrow 5{{t}^{2}}-12t-81=0\]
\[\Rightarrow \,\,t=\frac{12\pm \sqrt{144+1620}}{10}=\frac{12\pm \sqrt{1764}}{10}\approx 5.4\,\sec .\]
Problem 65. A particle is dropped under gravity from rest from a height \[h\,(g=9.8\,m/{{s}^{2}})\]and it travels a distance 9h/25 in the last second, the height h is [MNR 1987]
(a) 100 m (b) 122.5 m (c) 145 m (d) 167.5 m
Solution: (b) Distance travelled in \[n\] \[\sec =\frac{1}{2}g{{n}^{2}}= h\] ..... (i)
Distance travelled in \[{{n}^{th}}\sec =\frac{g}{2}(2n-1)=\frac{9h}{25}\] ..... (ii)
Solving (i) and (ii) we get. \[h=122.5\,m\].
Problem 66. A stone thrown upward with a speed u from the top of the tower reaches the ground with a velocity 3u. The height of the tower is [EAMCET 1983; RPET 2003]
(a) \[3{{u}^{2}}/g\] (b) \[4{{u}^{2}}/g\] (c) \[6{{u}^{2}}/g\] (d) \[9{{u}^{2}}/g\]
Solution: (b) For vertical downward motion we will consider initial velocity = – u
By applying \[{{v}^{2}}={{u}^{2}}+2gh,\,\,\,{{(3u)}^{2}}={{(-u)}^{2}}+2gh\Rightarrow \,h=\frac{4{{u}^{2}}}{g}\]
Problem 67. A stone dropped from the top of the tower touches the ground in 4 sec. The height of the tower is about [MP PET 1986; AFMC 1994; CPMT 1997; BHU 1998; DPMT 1999; RPET 1999]
(a) 80 m (b) 40 m
(c) 20 m (d) 160 m
Solution: (a) \[h=\frac{1}{2}g{{t}^{2}}=\frac{1}{2}\times 10\times {{4}^{2}}=80\,m.\]
Problem 68. A body is released from a great height and falls freely towards the earth. Another body is released from the same height exactly one second later. The separation between the two bodies, two seconds after the release of the second body is [CPMT 1983; Kerala PMT 2002]
(a) 4.9 m (b) 9.8 m
(c) 19.6 m (d) 24.5 m
Solution: (d) The separation between two bodies, two second after the release of second body is given by:
\[\operatorname{s} =\frac{1}{2}g(t_{1}^{2}-t_{2}^{2})=\frac{1}{2}\times 9.8\times ({{3}^{2}}-{{2}^{2}})=24.5\,m\]
You need to login to perform this action.
You will be redirected in
3 sec
