10th Class Mathematics Some Applications of Trigonometry Question Bank

done Some Applications of Trigonometry Total Questions - 20

• question_answer1)
  A man is standing on the deck of a ship, which is 10 m above water level. He observes the angle of elevation of the top of a hill as \[{{45}^{o}}\] and the angle of depression of the base of the hill as \[{{30}^{o}}\]. Calculate the distance of the hill from the ship and the height of the hill.
  A)
   \[17.32m,\text{ }27.3m\] done clear
  B)
   \[18.32\text{ }m,\text{ }28.3\text{ }m\] done clear
  C)
   \[17.89\text{ }m,\text{ }28.3\text{ }m\] done clear
  D)
   \[8.32\text{ }m,\text{ }29.2\text{ }m\] done clear
  View Solution play_arrow

• question_answer2)
  A vertical tower stands on a horizontal land and is surmounted by a vertical flag staff of height 12 metres. At a point on the plane, the angle of elevation of the bottom and the top of the flag staff are respectively \[{{45}^{o}}\] and \[{{60}^{o}}\]. Find the height of tower.
  A)
   \[6\left( \sqrt{3}+4 \right)\,m\]            done clear
  B)
   \[6\left( \sqrt{3}+1 \right)\,m\] done clear
  C)
          \[7\left( \sqrt{3}+1 \right)\,m\]    done clear
  D)
          None of these done clear
  View Solution play_arrow

• question_answer3)
  Solve :

  (i) A tower is 50 m high. Its shadow is x m shorter when the Sun's altitude is \[{{45}^{o}}\]than when it is \[{{30}^{o}},\] then x = ___.

  (ii)The angle of elevation of the top of a tower from a point 100 m from the tower is \[{{45}^{o}}\] then the height of the tower is __.

  A)

  	(i)	(ii)
  	\[\begin{array}{*{35}{l}}    38.6\,m~  \\ \end{array}\]	102m

                  done clear
  B)

  	(i)	(ii)
  	\[36.6\,m\]	100m

                  done clear
  C)

  	(i)	(ii)
  	\[36.1\text{ }m\]	98m

                  done clear
  D)

  	(i)	(ii)
  	\[39.6\,m\]	101m

  done clear
  View Solution play_arrow

• question_answer4)
  A player sitting on the top of a tower of height 40 m observes the angle of depression of a bail lying on the ground is \[{{60}^{o}}\]. The distance between the foot of the tower and the ball is
  A)
   \[\frac{50}{\sqrt{3}}m\]                    done clear
  B)
   \[\frac{40}{\sqrt{3}}m\]        done clear
  C)
          \[40\sqrt{3}\,m\]         done clear
  D)
          \[50\sqrt{3}\,m\]         done clear
  View Solution play_arrow

• question_answer5)
  A straight tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle of \[{{30}^{o}}\] with the ground. The distance from the foot of the tree to the point, where the top touches the ground is 10 m. The height of the tree is _____.
  A)
   \[10\sqrt{3}\,m\]        done clear
  B)
   \[\frac{10\sqrt{3}\,}{3}m\]    done clear
  C)
          \[10(\sqrt{3}+1)m\]     done clear
  D)
          \[10(\sqrt{3}-1)m\] done clear
  View Solution play_arrow

• question_answer6)
  Amit is standing on the ground and flying a kite with 100 m of string at an elevation of \[{{30}^{o}}\]. Another boy, Nitin is standing on the roof of a 10 m high building and is flying his kite at an elevation of \[{{45}^{o}}\]. Both Amit and Nitin are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
  A)
   \[40\sqrt{2}\,m\]        done clear
  B)
   \[50\sqrt{3}\,m\]         done clear
  C)
          \[42\sqrt{3}\,m\]        done clear
  D)
          \[41\sqrt{2}\,m\]                     done clear
  View Solution play_arrow

• question_answer7)
  The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of \[{{30}^{o}}\] with horizontal, then the length of the wire is _____.
  A)
   12m                            done clear
  B)
   10m                done clear
  C)
   8m                  done clear
  D)
          6 m done clear
  View Solution play_arrow

• question_answer8)
                          There is a small island in the middle of a 50 m wide river and a tall tree stands on the island. P and Q are points directly opposite to each other on the two banks, and in line with the tree. If the angles of elevation of the top of the tree from P and Q are respectively \[{{60}^{o}}\] and \[{{30}^{o}},\] find the height of the tree.                      
  A)
  \[23.56\text{ }m\]                    done clear
  B)
   \[21.65\text{ }m\]       done clear
  C)
          \[22.69\text{ }m\]         done clear
  D)
          \[22.65\text{ }m~\]    done clear
  View Solution play_arrow

• question_answer9)
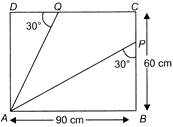
  In the given figure, ABCD is a rectangle in which segments AP and AQ are drawn as shown. Then the length of \[(AP+AQ)\]is  '
  A)
   300 cm           done clear
  B)
   350 cm           done clear
  C)
   320 cm        done clear
  D)
   360 cm                       done clear
  View Solution play_arrow

• question_answer10)
  The shadow of a tower, when the angle of elevation of the sun is \[{{45}^{o}}\] is found to be 15 metres longer than when it is \[{{60}^{o}}\]. Find the height of the tower.           
  A)
   \[35.92\text{ }m\]                   done clear
  B)
  \[36.59\text{ }m\]      done clear
  C)
          \[35.49\text{ }m\]        done clear
  D)
          \[37.49\text{ }m\]      done clear
  View Solution play_arrow

• question_answer11)
  A person observed the angle of elevation of the top of a tower as \[{{30}^{o}}\]. He walked 10 m towards the foot of the tower along ground level and found the angle of elevation of the top of the tower as \[{{60}^{o}}\]. Find the height of the tower.
  A)
   \[9.66\text{ }m\]                     done clear
  B)
   \[7.89\text{ }m\]         done clear
  C)
   \[8.66\text{ }m\]        done clear
  D)
   \[7.64\text{ }m\] done clear
  View Solution play_arrow

• question_answer12)
  The angle of elevation of a cloud from a point h metres above a lake is \[\theta \]. The angle of depression of its reflection in the lake is\[{{45}^{o}}\]. The height of the cloud is ____.
  A)
   \[\frac{h(1+\tan \theta )}{(1-\tan \theta )}\] done clear
  B)
   \[\frac{h(1-\tan \theta )}{1+\tan \theta }\] done clear
  C)
   \[h\,\tan \,({{45}^{o}}-\theta )\] done clear
  D)
     None of these done clear
  View Solution play_arrow

• question_answer13)
  The top of a broken tree has its top end touching the ground at a distance 15 m from the bottom, the angle made by the broken end with the ground is \[{{30}^{o}}\]. Then length of broken part is
  A)
  \[10\text{ }m\]                         done clear
  B)
   \[\sqrt{3}\text{ }m\]   done clear
  C)
          \[5\sqrt{3}\text{ }m\]         done clear
  D)
          \[10\sqrt{3}\text{ }m\]                       done clear
  View Solution play_arrow

• question_answer14)
  The shadow of a tower, when the angle of elevation of the sun is \[{{45}^{o}},\] is found to be 10 metres longer than when the angle of elevation is \[{{60}^{o}}\]. Find the height of the tower. [Given : \[\sqrt{3}=1.732\]]
  A)
   \[22.66\text{ }m\]                   done clear
  B)
   \[23\text{ }m\]            done clear
  C)
   \[23.66\text{ }m\]      done clear
  D)
   \[22.16\text{ }m\] done clear
  View Solution play_arrow

• question_answer15)
  Two persons are 'a' metres apart and the height of one is double that of the other. If from the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary, then the height of the shorter person in metres is ______.
  A)
   \[\frac{a}{4}\]                                    done clear
  B)
   \[\frac{a}{\sqrt{2}}\]             done clear
  C)
          \[a\sqrt{2}\]    done clear
  D)
          \[\frac{a}{2\sqrt{2}}\] done clear
  View Solution play_arrow

• question_answer16)
  Two stations due south of a leaning tower, which leans towards the north, are at distances a and b from its foot. If x and y are the angles of elevations of the top of the tower from these stations then its  inclination \[\theta \] to the horizontal is given by \[\cot \theta =\]
  A)
   \[\frac{b\,\cot x+a\,\cot y}{b-a}\] done clear
  B)
   \[\frac{b\,\cot x-a\,\cot y}{b-a}\] done clear
  C)
   \[\frac{a\,\cot x-b\,\cot y}{b+a}\] done clear
  D)
   None of these done clear
  View Solution play_arrow

• question_answer17)
  If the angle of elevation of a cloud from a point h metres above a lake is x and the angle of depression of its reflection in the lake is y, then the distance of the cloud from the point of observation is
  A)
   \[\frac{2h\,\sec \,x}{\tan y+\tan x}\]  done clear
  B)
   \[\frac{2h\,cos\,x}{\tan x+\tan \,y}\] done clear
  C)
                      \[\frac{2h\,cot\,x}{\tan \,y+\tan \,x}\] done clear
  D)
          \[\frac{2h\,\sec \,x}{\tan \,y-\tan \,x}\] done clear
  View Solution play_arrow

• question_answer18)
  The angle of elevation of a cliff from a fixed point A is \[{{45}^{o}}\]. After going up a distance of 600 metres towards the top of the cliff at an inclination of \[{{30}^{o}},\] it is found that the angle of elevation is \[{{60}^{o}}\]. Find the height of the cliff.
  A)
  \[817.8\text{ }m\]                    done clear
  B)
   \[818.5\text{ }m\]       done clear
  C)
          \[820.5\text{ }m\]        done clear
  D)
          \[819.6\text{ }m\] done clear
  View Solution play_arrow

• question_answer19)
  The angle of elevation of an aeroplane from a point on the ground is \[{{45}^{o}}\]. After a flight of 10 sec, the elevation changes to \[{{30}^{o}}\]. If the aeroplane is flying at a height of 3 km, find the speed of the aeroplane.
  A)
   \[785.46\text{ }km/hr\]           done clear
  B)
   \[790.56\text{ }km/hr\]                       done clear
  C)
   \[780.56\text{ }km/hr\]           done clear
  D)
   \[782.65\text{ }km/hr\]           done clear
  View Solution play_arrow

• question_answer20)
  The angle of depressions of the top and bottom of 10 m tall building from the top of a multistoried building are \[{{30}^{o}}\] and \[{{60}^{o}}\] respectively. Find the height of the multistoried building and the distance between the two buildings.
  A)
   \[15\,m,\,\,5\sqrt{3}\,m\]   done clear
  B)
          \[15\,m,\,\,6\sqrt{3}\,m\] done clear
  C)
          \[16\,m,\,\,4\sqrt{3}\,m\]   done clear
  D)
          \[16\,m,\,\,5\sqrt{3}\,m\] done clear
  View Solution play_arrow