7th Class Mathematics Practical Geometry Question Bank

done Practical Geometry

• question_answer1) In \[\Delta ABC,\]if \[AB=7\text{ }cm,\text{ }\angle A={{40}^{o}}\]and \[\angle B={{70}^{o}}\],which criterion can be used to construct this triangle?

  A) ASA done clear

  B) SSS done clear

  C) SAS done clear

  D) RHS done clear

  View Solution play_arrow

• question_answer2) Which one of the following is true for the given triangle?

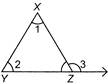
  A) \[\angle 3=\angle 1+\angle 2\] done clear

  B) \[\angle 1=\angle 3+\angle 2\] done clear

  C) \[\angle 2=\angle 1+\angle 3\] done clear

  D) Both (a) and (b) done clear

  View Solution play_arrow

• question_answer3) The __ criterion is used to construct a triangle when the lengths of the three sides are given.

  A) SAS done clear

  B) SSS done clear

  C) RHS done clear

  D) ASA done clear

  View Solution play_arrow

• question_answer4) A triangle can be constructed by taking its sides as

  A) \[1.8\text{ }cm,\text{ }2.6\text{ }cm,\text{ }4.4\text{ }cm\] done clear

  B) \[2\text{ }cm,\text{ }3\text{ }cm,\text{ }4\text{ }cm\] done clear

  C) \[2.4\text{ }cm,\text{ }2.4\text{ }cm,\text{ }6.4\text{ }cm\] done clear

  D) \[3.2\text{ }cm,\text{ }2.3\text{ }cm,\text{ }5.5\text{ }cm\] done clear

  View Solution play_arrow

• question_answer5) A triangle can be constructed by taking two of its angles as

  A) \[{{110}^{o}},\text{ }{{40}^{o}}\] done clear

  B) \[{{70}^{o}},{{115}^{o}}\] done clear

  C) \[{{135}^{o}},{{45}^{o}}\] done clear

  D) \[{{90}^{o}},{{90}^{o}}\] done clear

  View Solution play_arrow

• question_answer6) Which of the following sets of triangles could be the lengths of the sides of a right-angled triangle?

  A) \[3\text{ }cm,\text{ }4\text{ }cm,\text{ }6\text{ }cm\] done clear

  B) \[9\text{ }cm,\text{ }16\text{ }cm,\text{ }26\text{ }cm\] done clear

  C) \[1.5\text{ }cm,\text{ }3.6\text{ }cm,\text{ }3.9\text{ }cm\] done clear

  D) \[7\text{ }cm,\text{ }24\text{ }cm,\text{ }26\text{ }cm\] done clear

  View Solution play_arrow

• question_answer7) In which of the following cases, a unique triangle can be drawn?

  A) \[AB=4\text{ }cm,\text{ }BC=8\text{ }cm\]and \[CA=2\text{ }cm\] done clear

  B) \[BC=5.2\text{ }cm,\text{ }\angle S={{90}^{o}}\]and \[\angle C={{110}^{o}}\] done clear

  C) \[XY=5\text{ }cm,\text{ }\angle X={{45}^{o}}\]and \[\angle Y={{60}^{o}}\] done clear

  D) An isosceles triangle with the length of each equal side 6.2 cm. done clear

  View Solution play_arrow

• question_answer8) Which of the following statements is INCORRECT?

  A) If length of any two sides of a triangle are 7 cm and 10 cm, then length of its third side lies between 3 cm and 17 cm. done clear

  B) It is possible to construct a unique triangle if all its three angles are given. done clear

  C) An angle of \[\left( 7\frac{{{1}^{o}}}{2} \right)\] can't be constructed using compasses and ruler. done clear

  D) None of these done clear

  View Solution play_arrow

• question_answer9) Which of the following steps is INCORRECT while constructing \[\Delta XYZ\]if it is given that \[XY=6cm,\angle ZXy={{30}^{o}}\]and \[\angle XYZ={{100}^{o}}\]

  Step 1: Draw line XV of length 6 cm.

  Step 2: At X, draw a ray XP making an angle of \[{{30}^{o}}\]with XY.

  Step 3: At V, draw a ray YQ making an angle of \[{{100}^{o}}\] with YX.

  Step 4: The point of intersection of the two rays XY and YQ is Z.

  A) Step 1 done clear

  B) Step 2 and Step 4 done clear

  C) Step 3 done clear

  D) Step 4 done clear

  View Solution play_arrow

• question_answer10) Arrange the given steps in CORRECT order, while constructing \[\Delta \,PQR\]where \[PM\bot QS\]and it is given that \[QR=4.2\text{ }cm,\]\[\angle Q={{120}^{o}}\] and \[PQ=3.5\text{ }cm.\]

  Step 1. Now, extend RQ to S and with P as centre and with a sufficient radius, draw an arc, cutting SO at A and 8.

  Step 2. Along QX, set off \[QP=3.5\text{ }cm.\]

  Step 3. Draw a line segment \[QR=4.2\text{ }cm\]and construct\[\angle RQX={{120}^{o}}\].

  Step 4. Joint PR.

  Step 5. Joint PC, meeting RQ product at

  M. Then. \[PM\bot QS\]

  Step 6. With A as centre and radius more than half AB, draw an arc. Now with B as centre and with the same radius draw another arc, cutting the previous arc at C.

  A) 1\[\to \]2\[\to \]3\[\to \]4\[\to \]5\[\to \]6 done clear

  B) 4\[\to \]1\[\to \]2\[\to \]3\[\to \]5\[\to \]6 done clear

  C) 2\[\to \]4\[\to \]3\[\to \]1\[\to \]5\[\to \]6 done clear

  D) 3\[\to \]2\[\to \]4\[\to \]1\[\to \]6\[\to \]5 done clear

  View Solution play_arrow

• question_answer11) State 'T' for true and 'F' for false.

  (1) In a triangle, the measure of exterior angle is equal to the sum of the measure of interior opposite angles.

  (2) The sum of the measures of the three angles of a triangle is\[{{90}^{o}}\].

  (3) A perpendicular is always at \[{{90}^{o}}\] to a given line or surface.

  A)

  (1)	(2)	(3)
  T	T	F

  done clear

  B)

  (1)	(2)	(3)
  T	F	F

  done clear

  C)

  (1)	(2)	(3)
  T	F	T

  done clear

  D)

  (1)	(2)	(3)
  F	T	F

  done clear
  View Solution play_arrow

• question_answer12) Which of the following steps is INCORRECT while constructing \[\Delta LMA,\]right angled at M, given that \[LN=5\text{ }cm\]and\[MN=3\text{ }cm\]?

  Step 1. Draw MN of length 3 cm.

  Step 2. At M, draw MX1MN. (L should be somewhere on this perpendicular).

  Step 3. With N as centre, draw an arc of radius 5 cm. (L must be on this arc, since it is at a distance of 5 cm from N).

  Step 4. L has to be on the perpendicular line MX as well as on the arc drawn with centre N. Therefore, L is the meeting point of these two and ALMA/ is obtained.

  A) Only Step 4 done clear

  B) Both Step 2 and Step 3 done clear

  C) Only Step 2 done clear

  D) None of these done clear

  View Solution play_arrow

• question_answer13) Arrange the steps marked (i) to (v) In CORRECT order while constructing a line parallel to a given line, through a point not on the line using ruler and compasses only.

  Step 1. Take a line 'l' and a point ?A? outside ?l?.

  Step 2. Take any point Son l and join 8 to A

  (i) Now with A as centre and the same radius as in previous step, draw an arc EF cutting AB at G.

  (ii) With the same opening as in previous step and with G as centre, draw an arc cutting the arc EF at H.

  (iii) With B as centre and a convenient radius, draw an arc cutting l at C and BA at D,

  (iv) Now, join AH to draw a line W.

  A) (i)\[\to \](ii)\[\to \](iv)\[\to \](iii) done clear

  B) (iii)\[\to \](i)\[\to \](ii)\[\to \](iv) done clear

  C) (iii)\[\to \](ii)\[\to \](i)\[\to \](iv) done clear

  D) (i)\[\to \](ii)\[\to \](iii)\[\to \](iv) done clear

  View Solution play_arrow