9th Class Mathematics Circles Question Bank

done Circle Total Questions - 30

• question_answer1)
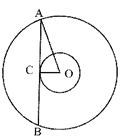
  In the given figure below, A chord AB of a circle \[{{\mathbf{C}}_{\mathbf{1}}}\] of radius \[\left( \sqrt{\mathbf{2}}\mathbf{+1} \right)\]cm touches a circle\[{{\mathbf{C}}_{2}}\]which is concentric to\[{{\mathbf{C}}_{1}}\]. If the radius of \[{{\mathbf{C}}_{2}}\] is \[\left( \sqrt{\mathbf{2}}\mathbf{-1} \right)\] cm. The length of AB is:
  A)
   \[3\sqrt[4]{3}\]cm          done clear
  B)
   \[6\sqrt{3}\]cm         done clear
  C)
   \[4\sqrt[4]{2}\]cm     done clear
  D)
   \[4\sqrt{3}\] cm done clear
  View Solution play_arrow

• question_answer2)
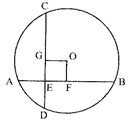
  In the given figure below, Chords AB and CD of a circle intersect at E and are perpendicular to each other. Segments AE, EB and ED are of lengths 2 cm, 6 cm and 3 cm respectively. Then the length of the diameter of the circle (in cm) is
  A)
   \[\sqrt{65}\]       done clear
  B)
   \[\frac{1}{2}\sqrt{65}\]          done clear
  C)
   65                                done clear
  D)
   \[\frac{65}{2}\] done clear
  View Solution play_arrow

• question_answer3)
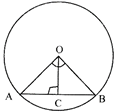
  In the given figure below. The angle subtended by a chord at its centre is\[\mathbf{12}{{\mathbf{0}}^{{}^\circ }}\], then the ratio between chord and radius is
  A)
  1 : 2                              done clear
  B)
  1 : 1 done clear
  C)
  \[\sqrt{2}:1\]                       done clear
  D)
  \[\sqrt{3}:1\] done clear
  View Solution play_arrow

• question_answer4)
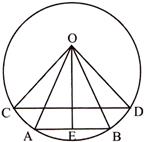
  In the given figure below, two chords of lengths x metre and y metre subtend angles \[\mathbf{6}{{\mathbf{0}}^{{}^\circ }}\] and \[\mathbf{9}{{\mathbf{0}}^{{}^\circ }}\] at the centre of the circle respectively. Which of the following is true?
  A)
   \[{{y}^{2}}=2{{x}^{2}}\]     done clear
  B)
   \[{{x}^{2}}=2{{y}^{2}}\] done clear
  C)
   \[{{x}^{2}}=4{{y}^{2}}\]                            done clear
  D)
   \[{{y}^{2}}=4{{x}^{2}}\] done clear
  View Solution play_arrow

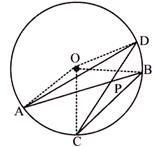
• question_answer5)
  In the given figure below, two chords AB and CD of a circle with centre O, intersect each other at P. If \[\angle \mathbf{AOD}=\mathbf{12}{{\mathbf{0}}^{{}^\circ }}\]and \[\angle \mathbf{BOC}=\mathbf{5}{{\mathbf{0}}^{{}^\circ }}\], then the value of \[\angle \mathbf{APC}\] is
  A)
   \[{{80}^{{}^\circ }}\]                        done clear
  B)
   \[{{75}^{{}^\circ }}\] done clear
  C)
   \[{{85}^{{}^\circ }}\]                                    done clear
  D)
   \[{{95}^{{}^\circ }}\] done clear
  View Solution play_arrow

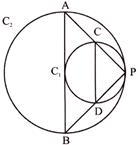
• question_answer6)
  In the given figure below, two circles \[{{C}_{1}}\] and \[{{C}_{2}}\] touch each other internally at P. Two lines PCA and PCB meet the circles \[{{\mathbf{C}}_{1}}\] in C, D and \[{{\mathbf{C}}_{2}}\] in A, B respectively. If \[\angle \mathbf{BDC}=\mathbf{13}{{\mathbf{0}}^{{}^\circ }}\], then the value of \[\angle \]ABP is equal to
  A)
   \[{{50}^{{}^\circ }}\]    done clear
  B)
   \[{{80}^{{}^\circ }}\] done clear
  C)
   \[{{100}^{{}^\circ }}\]                           done clear
  D)
   \[{{120}^{{}^\circ }}\] done clear
  View Solution play_arrow

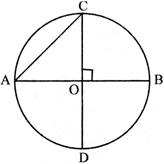
• question_answer7)
  In the given figure below, a circle with centre O. AB and CD are its two diameters perpendicular to each other. The length of chord AC is
  A)
   2 AB                            done clear
  B)
   \[\sqrt{2}AB\] done clear
  C)
   \[\frac{1}{2}AB\]                                  done clear
  D)
   \[\frac{1}{\sqrt{2}}AB\] done clear
  View Solution play_arrow

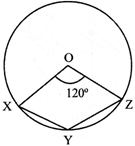
• question_answer8)
  In the adjoining figure \[\angle XOZ={{120}^{{}^\circ }}\]where O is the centre of the circle then \[\angle \mathbf{XYZ}\] is equal to
  A)
   \[{{110}^{{}^\circ }}\]                       done clear
  B)
   \[{{120}^{{}^\circ }}\]    done clear
  C)
   \[{{90}^{{}^\circ }}\]                                    done clear
  D)
   \[{{40}^{{}^\circ }}\] done clear
  View Solution play_arrow

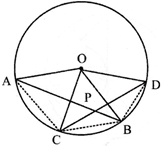
• question_answer9)
  In the given figure below, two chords AB and CD of a circle with centre O intersect at P. If \[\angle \mathbf{APC}=\mathbf{3}{{\mathbf{0}}^{{}^\circ }}\]. Then the value of \[\angle \mathbf{AOC}+~\angle \mathbf{BOD}\] is
  A)
   \[{{50}^{{}^\circ }}\]                           done clear
  B)
   \[{{60}^{{}^\circ }}\] done clear
  C)
   \[{{80}^{{}^\circ }}\]                                    done clear
  D)
   \[{{120}^{{}^\circ }}\] done clear
  View Solution play_arrow

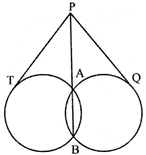
• question_answer10)
  In the given figure below. Two circles intersect at A and B. P is a point on produced RA. PT and PQ are tangents to Itie circles. The relation of PT and PQ is
  A)
   \[PT=2PQ\]               done clear
  B)
   \[PT<PQ\] done clear
  C)
   \[PT>PQ\]                    done clear
  D)
   \[PT=PQ\] done clear
  View Solution play_arrow

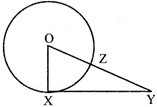
• question_answer11)
  In the given figure below. The length of a tangent from an external, point to a circle is \[5\sqrt{3}\] unit. if radius of the circle m 5 units, then the distance of the point from the circle is
  A)
   5 units              done clear
  B)
   15 units done clear
  C)
   -5 units                         done clear
  D)
   -15 units done clear
  View Solution play_arrow

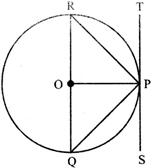
• question_answer12)
  In the given figure below, ST is a tangent to the circle at F and QR h a diameter of the circle. If\[\angle RPT={{55}^{{}^\circ }}\], then the value of \[\angle SPC\]is
  A)
   \[{{35}^{{}^\circ }}\]         done clear
  B)
   \[{{60}^{{}^\circ }}\] done clear
  C)
   \[{{80}^{{}^\circ }}\]                                    done clear
  D)
   \[{{100}^{{}^\circ }}\] done clear
  View Solution play_arrow

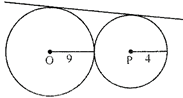
• question_answer13)
  In the given figure below, two circles with their centres at O and P and radii 9 cm and 4 cm respectively touch each other externally. The length of their common tangent is
  A)
   8.5 cm.                        done clear
  B)
   \[\frac{8}{\sqrt{2}}\] cm. done clear
  C)
   \[8\sqrt{2}\]cm.                         done clear
  D)
   12cm. done clear
  View Solution play_arrow

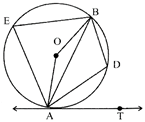
• question_answer14)
  In the given figure below, AB is a chord of a circle with centre O. A tangent AT is drawn at point A so that \[\angle \mathbf{BAT}\text{ }=\mathbf{4}{{\mathbf{0}}^{{}^\circ }}\]. Then \[\angle \mathbf{ADB}=\]?
  A)
   \[{{120}^{{}^\circ }}\]                      done clear
  B)
   \[{{130}^{{}^\circ }}\] done clear
  C)
   \[{{140}^{{}^\circ }}\]          done clear
  D)
   \[{{150}^{{}^\circ }}\] done clear
  View Solution play_arrow

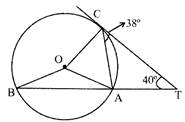
• question_answer15)
  In the given figure below, A, B and C are three points on a circle with centre O. The tangent at C meets BA produced to T. If  \[\angle \mathbf{ATC}=\mathbf{4}{{\mathbf{0}}^{{}^\circ }}\]and \[\angle \mathbf{ACT}=\mathbf{3}{{\mathbf{8}}^{{}^\circ }}\], then what is the value of \[\angle \mathbf{AOB}\]?
  A)
   \[{{78}^{{}^\circ }}\]                            done clear
  B)
   \[{{96}^{{}^\circ }}\] done clear
  C)
   \[{{102}^{{}^\circ }}\]                                   done clear
  D)
   \[{{128}^{{}^\circ }}\] done clear
  View Solution play_arrow

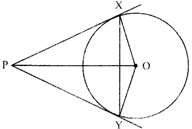
• question_answer16)
  In the given figure below, If PX and PY are tangents to the circle with centre O that \[\angle \mathbf{XPY}=\mathbf{4}{{\mathbf{0}}^{{}^\circ }}\], then \[\angle \mathbf{OXY}\] is equal to
  A)
   \[{{20}^{{}^\circ }}\]  done clear
  B)
   \[{{30}^{{}^\circ }}\] done clear
  C)
   \[{{40}^{{}^\circ }}\]                                    done clear
  D)
   \[{{50}^{{}^\circ }}\] done clear
  View Solution play_arrow

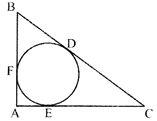
• question_answer17)
  In the given figure, an in-circle DEF is circumscribed by the right angled triangle in which AF = 6 cm and EC = 15 cm. Then the difference between CD and BD is
  A)
   1 cm.    done clear
  B)
   3 cm. done clear
  C)
   4 cm.                           done clear
  D)
   5 cm. done clear
  View Solution play_arrow

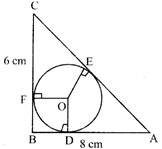
• question_answer18)
  In the given figure below, AABC is a right angled triangle with AB = 8 cm, BC = 6 cm. O is the in-centre of the triangle. The radius of the in-circle is
  A)
   3 cm                            done clear
  B)
   4 cm done clear
  C)
   2 cm     done clear
  D)
   5 cm done clear
  View Solution play_arrow

• question_answer19)
  Consider the following statements in respect of two chords XY and ZT of a circle intersecting at P.

  \[\mathbf{PZ}.\mathbf{PY}=\mathbf{PZ}.\mathbf{PT}\]

  PXZ and PTY are similar triangles.

  Which of the statements given above is/are correct?
  A)
   Only (i)                         done clear
  B)
   Only (ii)          done clear
  C)
   Both (i) and (ii)   done clear
  D)
   None done clear
  View Solution play_arrow

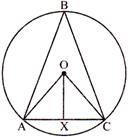
• question_answer20)
  In the given figure above, O is the centre of the circle, If \[OA=3cm,AC=3cm\] and OX is perpendicular to AC, \[\angle \mathbf{ABC}\] is equal to?
  A)
   \[{{60}^{{}^\circ }}\]                        done clear
  B)
   \[{{45}^{{}^\circ }}\]             done clear
  C)
   \[{{30}^{{}^\circ }}\]   done clear
  D)
   None of these done clear
  View Solution play_arrow

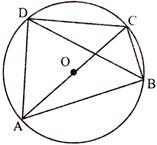
• question_answer21)
  AC is the diameter of the circumcircle of the cyclic quadrilateral ABCD. If. \[\angle \mathbf{BDC}=\mathbf{4}{{\mathbf{8}}^{{}^\circ }}\]then \[\angle \mathbf{ACB}\] is equal to
  A)
   \[{{42}^{{}^\circ }}\]       done clear
  B)
   \[{{45}^{{}^\circ }}\]            done clear
  C)
   \[{{48}^{{}^\circ }}\]                                    done clear
  D)
   \[{{58}^{{}^\circ }}\] done clear
  View Solution play_arrow

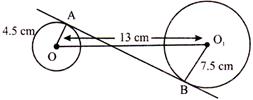
• question_answer22)
  The distance between the centre of two circles having radii 7.5 cm and 4.5 cm respectively is 13 cm. what is the length of the transverse common tangent of these circles?
  A)
   8 cm                            done clear
  B)
   7cm     done clear
  C)
   6 cm                            done clear
  D)
   5 cm done clear
  View Solution play_arrow

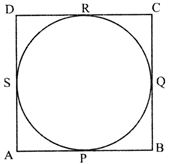
• question_answer23)
  ABCD is a quadrilateral, the sides of which touch a circle. Which one of the following is correct?
  A)
   \[AB+AD=CB+CD\]           done clear
  B)
   \[AB:CD=AD:BC\] done clear
  C)
   \[AB+CD=AD+BC\]   done clear
  D)
   \[AB:AD=CB:CD\] done clear
  View Solution play_arrow

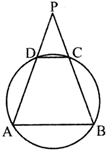
• question_answer24)
  In the given figure below, if \[\angle BAD={{50}^{{}^\circ }},\text{ }\angle ADC={{115}^{{}^\circ }}\] then \[\angle DPC\] is
  A)
   \[{{40}^{{}^\circ }}\]                        done clear
  B)
   \[{{65}^{{}^\circ }}\]     done clear
  C)
   \[{{50}^{{}^\circ }}\]                                    done clear
  D)
   \[{{60}^{{}^\circ }}\] done clear
  View Solution play_arrow

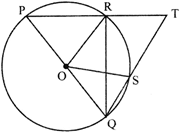
• question_answer25)
  In the given figure below. PQ is a diameter of the circle whose centre is at O. If \[\angle \mathbf{ROS}=\mathbf{4}{{\mathbf{6}}^{{}^\circ }}\]and OR is a bisector of \[\angle \mathbf{PQR}\], then \[\angle \mathbf{RTS}\] is equal to,
  A)
   \[{{46}^{{}^\circ }}\]                         done clear
  B)
   \[{{64}^{{}^\circ }}\] done clear
  C)
   \[{{69}^{{}^\circ }}\]                        done clear
  D)
   \[{{67}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer26)
  In the given figure below. O is the centre of the circle. AC and BD intersect at P. If \[\angle \mathbf{AOB}=\mathbf{11}{{\mathbf{0}}^{{}^\circ }}\] and \[\angle \mathbf{DAP}=\mathbf{3}{{\mathbf{0}}^{{}^\circ }}\], then \[\angle \mathbf{APB}\] is equal to
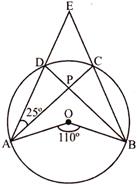
  A)
   \[{{77}^{{}^\circ }}\]                        done clear
  B)
   \[{{80}^{{}^\circ }}\]    done clear
  C)
   \[{{85}^{{}^\circ }}\]                                    done clear
  D)
   \[{{90}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer27)
  In the given figure, AB is a diameter of a circle and CD is perpendicular to AB, if AB=10 cm and \[AE=2\]cm, then what is the length of ED is
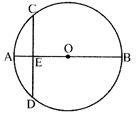
  A)
   5 cm                            done clear
  B)
   4cm       done clear
  C)
   10 cm                          done clear
  D)
   20 cm done clear
  View Solution play_arrow

• question_answer28)
  In the given figure above, O is the centre of the circle. The line UTV is a tangent to the circle at T, \[\angle \mathbf{VTR}=\mathbf{5}{{\mathbf{6}}^{{}^\circ }}\]and \[\Delta \mathbf{PTR}\] is an isosceles triangle such that TP = TR. \[\angle \mathbf{x}+\angle \mathbf{y}+\angle \mathbf{z}\]is equal to?
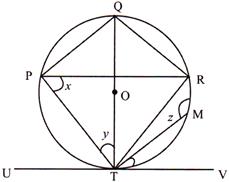
  A)
   \[{{175}^{{}^\circ }}\]                       done clear
  B)
   \[{{208}^{{}^\circ }}\]            done clear
  C)
   \[{{214}^{{}^\circ }}\]                                   done clear
  D)
   \[{{250}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer29)
  In the given figure above,\[\angle \mathbf{AOB}=\mathbf{4}{{\mathbf{8}}^{{}^\circ }}\], AC and OB Intersect each other at right angles. What is the measure of\[\angle \mathbf{OBC}\] (where, O is the centre of the circle)?
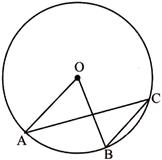
  A)
   \[{{44}^{{}^\circ }}\]                        done clear
  B)
   \[{{46}^{{}^\circ }}\]              done clear
  C)
   \[{{66}^{{}^\circ }}\]        done clear
  D)
   \[{{78.5}^{{}^\circ }}\] done clear
  View Solution play_arrow

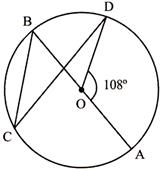
• question_answer30)
  In the figure given above O is the centre of the circle and\[\angle \mathbf{AOD}=\mathbf{10}{{\mathbf{8}}^{{}^\circ }}\], \[\angle \mathbf{BCD}\]is equal to
  A)
   \[{{53}^{{}^\circ }}\]                        done clear
  B)
   \[{{43}^{{}^\circ }}\]             done clear
  C)
   \[{{40}^{{}^\circ }}\]                        done clear
  D)
   \[{{36}^{{}^\circ }}\] done clear
  View Solution play_arrow