9th Class Mathematics Quadrilaterals Question Bank

done Quadrilateral Total Questions - 40

• question_answer1)
  Q is a point in the interior of a rectangle ABCD. If \[\mathbf{QA}=\mathbf{4}\]cm, \[QB=3\]cm and \[\mathbf{QC}=\mathbf{5}\] cm, then the length of QD (in cm) is
  A)
   \[4\sqrt{2}\] done clear
  B)
   \[5\sqrt{2}\] done clear
  C)
   \[\sqrt{34}\]                              done clear
  D)
   \[\sqrt{41}\] done clear
  View Solution play_arrow

• question_answer2)
  The length of the two adjacent sides of a rectangle inscribed in a circle are 3 cm and 4 cm respectively. Then the radius of the circle will be
  A)
   6 cm                            done clear
  B)
   2.5 cm done clear
  C)
   8 cm                            done clear
  D)
   8.5 cm done clear
  View Solution play_arrow

• question_answer3)
  PQRA is a rectangle, \[\mathbf{AP}=\mathbf{24}\]cm. \[\mathbf{PQ}=\mathbf{8}\]cm. \[\Delta \mathbf{ABC}\] is a triangle whose vertices lie on the sides of PQRA such that BQ = 2 cm and \[\mathbf{QC}=\mathbf{18}\]cm. Then the length of the line joining the mid points of the sides AB and BC is
  A)
   \[4\sqrt{2}\]cm.                         done clear
  B)
   5 cm done clear
  C)
   6 cm.                           done clear
  D)
   10 cm. done clear
  View Solution play_arrow

• question_answer4)
  The length of the diagonal BD of the parallelogram \[\Delta \mathbf{BCD}\] is 12 cm. If P and Q are the centroid of the \[\Delta \mathbf{ABC}\] and \[\Delta \mathbf{ADC}\] respectively then the length of the line segment PQ is
  A)
   4 cm                            done clear
  B)
   4 cm done clear
  C)
   9 cm                            done clear
  D)
   12 cm done clear
  View Solution play_arrow

• question_answer5)
  ABCD is a cyclic trapezium whose sides AD and BC are parallel to each other. If  \[\angle \mathbf{ABC}=\mathbf{7}{{\mathbf{5}}^{{}^\circ }}\], then the measure of the \[\angle \mathbf{BCD}\] is
  A)
   \[{{162}^{{}^\circ }}\]                       done clear
  B)
   \[{{18}^{{}^\circ }}\] done clear
  C)
   \[{{108}^{{}^\circ }}\]                       done clear
  D)
   \[{{75}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer6)
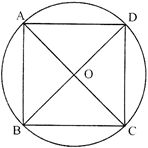
  ABCD is a cyclic quadrilateral and O is the centre of the circle. If \[\angle \mathbf{COD}=\mathbf{12}{{\mathbf{0}}^{{}^\circ }}\]and \[\angle \mathbf{BAC}=\mathbf{6}{{\mathbf{0}}^{{}^\circ }}\], then the value of \[\angle \mathbf{BCD}\] is equal to
  A)
   \[{{70}^{{}^\circ }}\]                                    done clear
  B)
   \[{{90}^{{}^\circ }}\] done clear
  C)
   \[{{60}^{{}^\circ }}\]      done clear
  D)
   \[{{80}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer7)
  ABCD is a cyclic quadrilateral and AD is a diameter. If \[\angle \mathbf{DAC}=\mathbf{6}{{\mathbf{5}}^{{}^\circ }}\] then value of \[\angle \mathbf{ABC}\] is
  A)
   \[{{55}^{{}^\circ }}\]                                    done clear
  B)
   \[{{35}^{{}^\circ }}\] done clear
  C)
   \[{{155}^{{}^\circ }}\]        done clear
  D)
   \[{{125}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer8)
  ABCD is a cyclic quadrilateral. AB and DC when produced meet at P, if \[PA=12\]cm., PB = 8 cm, PC = 6 cm, then the length (in cm ) of PD is
  A)
   8 cm                            done clear
  B)
   6cm done clear
  C)
   10 cm                          done clear
  D)
   16 cm done clear
  View Solution play_arrow

• question_answer9)
  In a cyclic quadrilateral ABCD, \[\angle BCD={{130}^{{}^\circ }}\]and passes through the centre of the circle. Then\[\angle \mathbf{ABD}=\]?
  A)
   \[{{30}^{{}^\circ }}\]                                    done clear
  B)
   \[{{40}^{{}^\circ }}\] done clear
  C)
   \[{{50}^{{}^\circ }}\]                                    done clear
  D)
   \[{{60}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer10)
  PQRS is a rhombus. A straight line through R cuts PS produced at X and PQ produced at Y. If \[SX=\frac{1}{2}PQ\], then the ratio of the length of QY and PQ is
  A)
   2:1  done clear
  B)
   1 : 2 done clear
  C)
   \[1:1\]                           done clear
  D)
   3:1 done clear
  View Solution play_arrow

• question_answer11)
  In a quadrilateral ABCD, the bisectors of \[\angle \mathbf{A}\] and \[\angle B\] meet at O. If \[\angle C={{80}^{{}^\circ }}\]and \[\angle \mathbf{D}=\mathbf{12}{{\mathbf{0}}^{{}^\circ }}\], then measure of \[\angle \mathbf{AOB}\] is
  A)
   \[{{40}^{{}^\circ }}\]                                    done clear
  B)
   \[{{60}^{{}^\circ }}\] done clear
  C)
   \[{{80}^{{}^\circ }}\]                           done clear
  D)
          \[{{100}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer12)
  If PQRS be a rhombus, PR is its smallest diagonal and \[\angle \mathbf{PQR}=\mathbf{6}{{\mathbf{0}}^{{}^\circ }}\], find length of a side of the rhombus when \[\mathbf{PR}=\mathbf{6}\]cm.
  A)
   6 cm    done clear
  B)
   3 cm done clear
  C)
   \[6\sqrt{2}\]cm                          done clear
  D)
   \[3\sqrt{3}\]cm done clear
  View Solution play_arrow

• question_answer13)
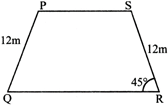
  PQRS is a trapezium in which \[\mathbf{PS}\parallel \mathbf{QR}\] and \[PQ=SR=12\]m. then the distance of PS from QR is:
  A)
   \[10\sqrt{2}\]m                       done clear
  B)
   \[4\sqrt{2}\]m done clear
  C)
   \[5\sqrt{2}\]m                        done clear
  D)
   \[6\sqrt{2}\]m done clear
  View Solution play_arrow

• question_answer14)
  In a trapezium ABCD If \[\mathbf{AB}\parallel \mathbf{CD}\], thee \[\mathbf{A}{{\mathbf{C}}^{2}}+\mathbf{B}{{\mathbf{D}}^{2}}\]is equal to:
  A)
   \[B{{C}^{2}}+A{{D}^{2}}+2AB.CD\]         done clear
  B)
   \[A{{B}^{2}}+C{{D}^{2}}+2AD.BC\] done clear
  C)
   \[A{{B}^{2}}+C{{D}^{2}}+2AB.CD\]           done clear
  D)
   \[B{{C}^{\mathbf{2}}}+A{{D}^{2}}+2BC.AD\] done clear
  View Solution play_arrow

• question_answer15)
  The parallel sides of a trapezium are x and y respectively. The line joining the points of its non-parallel sides will be:
  A)
   \[\sqrt{xy}\]                              done clear
  B)
   \[\frac{2xy}{x+y}\] done clear
  C)
   \[\frac{\left( x+y \right)}{2}\]   done clear
  D)
   \[\frac{1}{4}(x-y)\] done clear
  View Solution play_arrow

• question_answer16)
  ABCD is a trapezium in which \[\mathbf{AB}\parallel \mathbf{CD}\] and \[AB=3CD\]Its diagonals intersect other at O then the ratio of the areas of the triangles AOB and COD is:
  A)
   1 : 2                             done clear
  B)
   2 : 1              done clear
  C)
   9 : 1 done clear
  D)
   1 : 4 done clear
  View Solution play_arrow

• question_answer17)
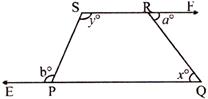
  The sides BA and DC of quadrilateral ABCD are produced as shown la figure. Them which of the following statements is correct?
  A)
   \[2{{x}^{{}^\circ }}+{{y}^{{}^\circ }}={{a}^{{}^\circ }}+{{b}^{{}^\circ }}\]             done clear
  B)
   \[{{x}^{{}^\circ }}+\frac{1}{2}{{y}^{{}^\circ }}=\frac{{{a}^{{}^\circ }}+{{b}^{{}^\circ }}}{2}\] done clear
  C)
   \[{{x}^{{}^\circ }}+{{y}^{{}^\circ }}={{a}^{{}^\circ }}+{{b}^{{}^\circ }}\]  done clear
  D)
   \[{{x}^{{}^\circ }}+{{a}^{{}^\circ }}={{y}^{{}^\circ }}+{{b}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer18)
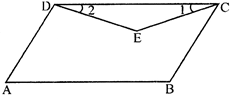
  In the quadrilateral ABCD, the line segments bisecting \[\angle \mathbf{C}\] and \[\angle D\] at E. Then the correct statement is:
  A)
   \[\angle A+\angle B=\angle CED\]             done clear
  B)
   \[\angle A+\angle B\text{=}2\angle CED\] done clear
  C)
   \[\angle A+\angle B=3\angle CED\]            done clear
  D)
   None of these done clear
  View Solution play_arrow

• question_answer19)
  If ABCD is a quadrilateral whose diagondals AC and BD intersect at O, then:
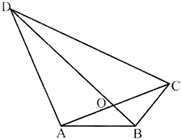
  A)
   \[\left( AB+BC+CD+DA \right)<\left( AC+BD \right)\] done clear
  B)
   \[\left( AB+BC+CD+DA \right)>2\left( AC+BD \right)\] done clear
  C)
   \[\left( AB+BC+CD+DA \right)>\left( AC+BD \right)\] done clear
  D)
   \[AB+BC+CD+DA=2\left( AC+BD \right)\] done clear
  View Solution play_arrow

• question_answer20)
  In the adjoining figure, ABCD is a quadrilateral in which AB is the longest side and CD is the shortest side, then:
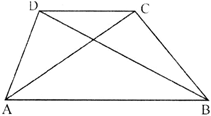
  A)
   \[\angle C>\angle A\text{ }and\text{ }\angle D>\angle B\]  done clear
  B)
   \[\angle C>\angle A\text{ }and\text{ }\angle B>\angle D\] done clear
  C)
   \[\angle C<A\text{ }and\text{ }\angle D<\angle B\]         done clear
  D)
   \[\angle C<\angle A\text{ }and\text{ }\angle D=\angle B\] done clear
  View Solution play_arrow

• question_answer21)
  In the given figure, ABCD is a square. A line segment DX cuts the side BC at X and the diagonal AC at 0 Such that \[\angle \mathbf{COD}=\mathbf{11}{{\mathbf{5}}^{{}^\circ }}\]and \[\angle \mathbf{OXC}={{\mathbf{x}}^{{}^\circ }}\]. The value of x is:
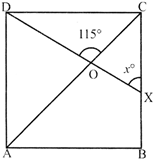
  A)
   \[{{40}^{{}^\circ }}\]                        done clear
  B)
   \[{{60}^{{}^\circ }}\] done clear
  C)
   \[{{80}^{{}^\circ }}\]                                    done clear
  D)
   \[{{85}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer22)
  In the given figure AE=BC and \[\mathbf{AE}\parallel \mathbf{BC}\] and the three sides AB, CD and ED are equal in length. If \[\mathbf{m}\angle \mathbf{A}=\mathbf{10}{{\mathbf{5}}^{{}^\circ }}\], find measures of \[\angle \,\mathbf{BCD}\]:
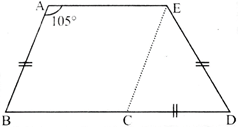
  A)
   \[{{138}^{{}^\circ }}\]                       done clear
  B)
   \[{{165}^{{}^\circ }}\] done clear
  C)
   \[{{88}^{{}^\circ }}\]                        done clear
  D)
   None of these done clear
  View Solution play_arrow

• question_answer23)
  A point X inside a rectangle PQRS is joined to the vertices then, which of the following is true?
  A)
   area\[\left( \Delta PSX \right)\]=area\[\left( \Delta PXQ \right)\] done clear
  B)
  \[area\left( \Delta PSX \right)+area\left( \Delta PXQ \right)=area\left( RSX \right)+area\left( \Delta RQX \right)\] done clear
  C)
   \[area\left( \Delta PXS \right)+area\left( \Delta RXQ \right)=area\left( \Delta SRX \right)+area\left( \Delta PXQ \right)\] done clear
  D)
   None of these done clear
  View Solution play_arrow

• question_answer24)
  In a rectangle ABCD, P, Q are the mid-points of BC and AD respectively and R is any point on PQ, then \[\Delta \mathbf{ARB}\] equals:
  A)
   \[\frac{1}{2}\left( [\,\,\,\,]\,ABCD \right)\] done clear
  B)
   \[\frac{1}{3}\left( [\,\,\,]\,ABCD \right)\] done clear
  C)
   \[\frac{1}{4}\left( [\,\,\,]\,ABCD \right)\] done clear
  D)
   None of these done clear
  View Solution play_arrow

• question_answer25)
  A quadrilateral is a parallelogram if:
  A)
   A pair of opposite sides is equal done clear
  B)
   A pair of opposite sides is equal and parallel done clear
  C)
   A pair of opposite sides is parallel done clear
  D)
   None of these done clear
  View Solution play_arrow

• question_answer26)
  In the adjoining figure, the value of x and y are:
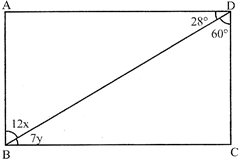
  A)
   \[{{5}^{{}^\circ }},{{4}^{{}^\circ }}\] done clear
  B)
   \[{{3}^{{}^\circ }},{{4}^{{}^\circ }}\] done clear
  C)
   \[{{2}^{{}^\circ }},{{1}^{{}^\circ }}\]                    done clear
  D)
   None of these done clear
  View Solution play_arrow

• question_answer27)
  In the adjoining figure ABCD is a parallelogram and E, F are the centroids of \[\Delta \mathbf{ABD}\] and \[\Delta \mathbf{BCD}\] respectively, then EF equals:
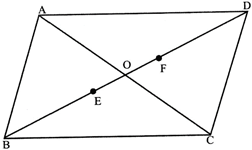
  A)
   AE                   done clear
  B)
   BE             done clear
  C)
   CE                               done clear
  D)
   DE done clear
  View Solution play_arrow

• question_answer28)
  In given figure, ABCD is a rhombus. If \[\angle OAB={{35}^{{}^\circ }}\], Then the value of x is
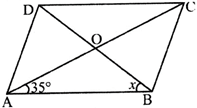
  A)
   \[{{25}^{{}^\circ }}\]                        done clear
  B)
   \[{{35}^{{}^\circ }}\]             done clear
  C)
   \[{{55}^{{}^\circ }}\]    done clear
  D)
   \[{{70}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer29)
  ABCD is a quadrilateral such that \[\angle \mathbf{D}=\mathbf{9}{{\mathbf{0}}^{{}^\circ }}\]. A circle C(O, r) touches the sides AB, BC, CD and DA at P, Q R and S respectively. If \[\mathbf{BC}=\mathbf{38}\]cm. \[\mathbf{CD}=\mathbf{25}\]cm and \[\mathbf{BP}=\mathbf{27}\]cm then radius 'r, is equal to
  A)
   14 cm  done clear
  B)
   11 cm          done clear
  C)
   12 cm                          done clear
  D)
   10 cm done clear
  View Solution play_arrow

• question_answer30)
  Find each interior and exterior angle of regular polygon having 30 sides.
  A)
   \[{{154}^{{}^\circ }},{{34}^{{}^\circ }}\]                           done clear
  B)
   \[{{168}^{{}^\circ }},{{12}^{{}^\circ }}\]    done clear
  C)
   \[{{122}^{{}^\circ }},{{15}^{{}^\circ }}\]               done clear
  D)
   \[{{121}^{{}^\circ }},{{58}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer31)
  In the given figure, ABCD is a parallelogram in which \[\angle \mathbf{BAD}=\mathbf{7}{{\mathbf{5}}^{{}^\circ }}\] and \[\angle CBD={{60}^{{}^\circ }}\]. Then, \[\angle \mathbf{BDC}=\]?
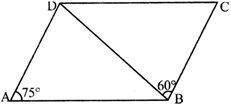
  A)
   \[{{60}^{{}^\circ }}\]                         done clear
  B)
   \[{{75}^{{}^\circ }}\] done clear
  C)
   \[{{45}^{{}^\circ }}\] done clear
  D)
   \[{{50}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer32)
  In a quadrilateral ABCD, If AO and BO are the bisectors of \[\angle \mathbf{A}\] and \[\angle B\] respectively \[\angle \mathbf{C}=\mathbf{3}{{\mathbf{0}}^{{}^\circ }}\]and\[\angle \mathbf{D}=\mathbf{7}{{\mathbf{0}}^{{}^\circ }}\]. Then, \[\angle \mathbf{AOB}=\]?
  A)
   \[{{40}^{{}^\circ }}\]                        done clear
  B)
   \[{{50}^{{}^\circ }}\] done clear
  C)
   \[{{80}^{{}^\circ }}\]                                    done clear
  D)
   \[{{100}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer33)
  The diagonals AC and BD of a parallelogram ABCD intersect each other at the O such that \[\angle \mathbf{DAC}=\mathbf{4}{{\mathbf{0}}^{{}^\circ }}\]and \[\angle \mathbf{AOB}=\mathbf{8}{{\mathbf{0}}^{{}^\circ }}\], Then \[\angle \mathbf{DBC}=\]?
  A)
   \[{{40}^{{}^\circ }}\]  done clear
  B)
   \[{{35}^{{}^\circ }}\]              done clear
  C)
   \[{{45}^{{}^\circ }}\]                                    done clear
  D)
   \[{{50}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer34)
  The lengths of the diagonals of a rhombus are 16 cm and 12 cm. The length of side of the rhombus is
  A)
   10 cm     done clear
  B)
   12 cm          done clear
  C)
   9 cm                            done clear
  D)
   8 cm done clear
  View Solution play_arrow

• question_answer35)
  The length of each side of a rhombus is 10 cm and of its diagonals 1$ of 16cm. The length of the other diagonal is
  A)
   13 cm                          done clear
  B)
   12 cm     done clear
  C)
   \[2\sqrt{39}\] cm           done clear
  D)
   6 cm done clear
  View Solution play_arrow

• question_answer36)
  In a rhombus ABCD,, its diagonal intersect at O then \[\angle \mathbf{AOB}\] is
  A)
   \[{{180}^{{}^\circ }}\]                       done clear
  B)
   \[{{0}^{{}^\circ }}\]              done clear
  C)
   \[{{90}^{{}^\circ }}\] done clear
  D)
   \[{{60}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer37)
  In. the adjoining kite, diagonals intersect at O If \[\angle ABO={{32}^{{}^\circ }}\] and \[\angle \left( OCD \right)=\mathbf{4}{{\mathbf{0}}^{{}^\circ }}\], \[\angle \mathbf{ABC}\]
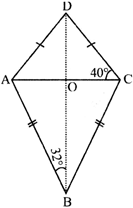
  A)
   \[{{60}^{{}^\circ }}\]                        done clear
  B)
   \[{{64}^{{}^\circ }}\]       done clear
  C)
   \[{{75}^{{}^\circ }}\]                                    done clear
  D)
   \[{{90}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer38)
  In the given figure, ABCD Is a \[\parallel \] gm and E is the mid-point of BC Also DE and AB when produced meet at F, Then,
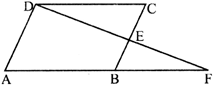
  A)
   \[AF=\frac{3}{2}AB\]               done clear
  B)
   \[AF=2AB\]      done clear
  C)
   \[AF=3AB\]                  done clear
  D)
   \[A{{F}^{2}}=2A{{B}^{2}}\] done clear
  View Solution play_arrow

• question_answer39)
  In the given figure, ABCD is a parallelogram, M is the mid-point of BD and BD bisects \[\angle B\] as well as \[\angle D\]. Then \[\angle AMB=\]?  
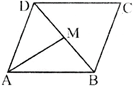
  A)
   \[{{45}^{{}^\circ }}\]                        done clear
  B)
   \[{{60}^{{}^\circ }}\] done clear
  C)
   \[{{90}^{{}^\circ }}\] done clear
  D)
   \[{{30}^{{}^\circ }}\] done clear
  View Solution play_arrow

• question_answer40)
  In the adjoining figure, AP and BP are angle bisectors of \[\angle \mathbf{A}\] and \[\angle B\] which meets At P in the parallelogram ABCD. Then\[\mathbf{2}\angle \mathbf{APB=?}\]                                
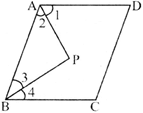
  A)
   \[\angle C+\angle D\]     done clear
  B)
   \[\angle A+\angle C\] done clear
  C)
   \[\angle B+\angle D\]                 done clear
  D)
   \[2\angle C\] done clear
  View Solution play_arrow