A) 2 sq. unit
B) 4 sq. unit
C) 8 sq. unit
D) None of these
Correct Answer: B
Solution :
We have \[y=\sin x\]| \[x\] | 0 | \[\pi /6\] | \[\pi /2\] | \[\pi \] | \[3\pi /2\] | \[2\pi \] |
| \[y\] | 0 | 0.5 | 1 | 0 | ?1 | 0 |
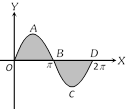 Required area = (area of \[OAB\]) + (area of\[BCD)\] = \[\int_{0}^{\pi }{\,y\,dx+\int_{\pi }^{2\pi }{(-y)\,dx}}\], (\[\because \] Area \[BCD\] is below \[x-\]axis) = \[\int_{0}^{\pi }{\sin x\,dx-\int_{\pi }^{2\pi }{\sin x\,dx=4}}\] sq. unit.
Required area = (area of \[OAB\]) + (area of\[BCD)\] = \[\int_{0}^{\pi }{\,y\,dx+\int_{\pi }^{2\pi }{(-y)\,dx}}\], (\[\because \] Area \[BCD\] is below \[x-\]axis) = \[\int_{0}^{\pi }{\sin x\,dx-\int_{\pi }^{2\pi }{\sin x\,dx=4}}\] sq. unit.
You need to login to perform this action.
You will be redirected in
3 sec
