A) \[\pi {{a}^{2}}\]
B) \[2\pi {{a}^{2}}\]
C) \[3\pi {{a}^{2}}\]
D) \[4\pi {{a}^{2}}\]
Correct Answer: A
Solution :
Since the curve is symmetrical about x-axis, therefore Required area\[A=2\int_{0}^{a}{a\sqrt{\frac{a-x}{x}}\,dx}\] Put \[x=a{{\sin }^{2}}\theta \] \[\Rightarrow dx=2a\sin \theta .\cos \theta \,d\theta \]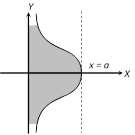 \[A=2\int_{0}^{\pi /2}{a\sqrt{\frac{a{{\cos }^{2}}\theta }{a{{\sin }^{2}}\theta }}}a\sin 2\theta \,d\theta \] \[=2{{a}^{2}}\int_{0}^{\pi /.2}{\frac{\cos \theta }{\sin \theta }2\sin \theta \cos \theta \,d\theta }\] \[A=4{{a}^{2}}\int_{0}^{\pi /2}{{{\cos }^{2}}\theta \,d\theta }\]Þ \[A=4{{a}^{2}}.\frac{1}{2}.\frac{\pi }{2}=\pi {{a}^{2}}\].
\[A=2\int_{0}^{\pi /2}{a\sqrt{\frac{a{{\cos }^{2}}\theta }{a{{\sin }^{2}}\theta }}}a\sin 2\theta \,d\theta \] \[=2{{a}^{2}}\int_{0}^{\pi /.2}{\frac{\cos \theta }{\sin \theta }2\sin \theta \cos \theta \,d\theta }\] \[A=4{{a}^{2}}\int_{0}^{\pi /2}{{{\cos }^{2}}\theta \,d\theta }\]Þ \[A=4{{a}^{2}}.\frac{1}{2}.\frac{\pi }{2}=\pi {{a}^{2}}\].
You need to login to perform this action.
You will be redirected in
3 sec
