question_answer

The area bounded by the curves \[y=\sqrt{x},\] \[2y+3=x\] and \[x-\]axis in the 1st quadrant is                    [IIT Screening 2003]

A)            9    

B)            \[\frac{27}{4}\]

C)            36  

D)            18

Correct Answer: A

Solution :

           Solving \[{{y}^{2}}=x\]and \[x=2y+3\]                    \[4{{y}^{2}}={{(x-3)}^{2}}\], \[4x={{x}^{2}}-6x+9\]                    Þ \[{{x}^{2}}-10x+9=0\]Þ \[(x-1)(x-9)=0\]Þ \[x=1,\,9\]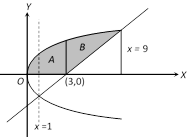        =\[-\,4\,[x\log x-x]_{0}^{1}=-4(-1)=4\]sq. unit,  \[(\because \text{ }\underset{\text{x}\to \text{0}}{\mathop{\text{lim}}}\,x\log x=0)\].       Required area = A+B\[=\int_{0}^{3}{\sqrt{x}dx+\int_{3}^{9}{\left[ \sqrt{x}-\left( \frac{x-3}{2} \right) \right]}}dx\]            \[=\frac{2}{3}[{{x}^{3/2}}]_{0}^{3}+\frac{2}{3}[{{x}^{3/2}}]_{3}^{9}-\frac{1}{2}\left[ \frac{{{x}^{2}}}{2}-3x \right]_{3}^{9}\]            \[=\frac{2}{3}3\sqrt{3}+\frac{2}{3}[9\times 3-3\sqrt{3}]-\frac{1}{2}\left[ \left( \frac{81}{2}-27 \right)-\left( \frac{9}{2}-9 \right) \right]\]            \[=18-\frac{1}{2}[36-18]=18-9=9\] sq. unit.