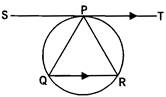
 Which of the following is correct statement?
Which of the following is correct statement?
A) P is equidistant from the extremities of the chord.
B) PT is the tangent parallel to the chord PQ.
C) PT is the tangent parallel to the cord PR.
D) S is equidistant from the extremities of the chord.
Correct Answer: A
Solution :
\[\therefore \] .....(1) (Angle between tangent and chord is equal to the angle in the alternate segment.) \[\text{224}=\text{12}0\times \text{1}+\text{1}0\text{4}\] ......(2) (Alternate angles as \[\text{12}0=\text{1}0\text{4}\times \text{1}+\text{16}\].) \[\text{1}0\text{4}=\text{16}\times \text{6}+\text{8}\] \[16=8\times 2+0\] ....... (2) [From statements 1 and 2.] \[\text{256}=\text{8}\times \text{32}+0\] PQ = PR \[3465={{3}^{2}}\times 5\times 7\times 11\] P is equidistant from Q and R, the extremities of the chord.You need to login to perform this action.
You will be redirected in
3 sec
