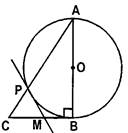
A) The tangent drawn to the circle at P bisects the side BC.
B) The tangent drawn to the circle at A bisects the side AB.
C) The tangent drawn to the circle at B bisects the side AC.
D) The tangent drawn to the circle at C bisects the side BC.
Correct Answer: A
Solution :
Join P to B. Now, \[=(\text{25}\times \text{7})\text{(2}\times {{\text{5}}^{\text{2}}}\times {{\text{7}}^{\text{3}}}\text{) c}{{\text{m}}^{\text{2}}}\] \[={{\text{2}}^{\text{6}}}\times {{\text{5}}^{\text{2}}}\times {{\text{7}}^{\text{4}}}\text{c}{{\text{m}}^{\text{2}}}\] But \[2-\sqrt{4}=2-2=0\] \[{{(\sqrt{5})}^{2}}=5\] \[\sqrt{9}-\sqrt{4}=3-2=1\] \[\sqrt{2}-\sqrt{3}\] (from \[1789=29x+49\]) \['x'\] \[\therefore \] \[1789-49=29x\] \[\Rightarrow \] MP=MC but, MP=MB MC = MB Hence, the statement in option [a] is true.You need to login to perform this action.
You will be redirected in
3 sec
