question_answer

The equation of the parabola whose focus is the point (0, 0) and the tangent at the vertex is \[x-y+1=0\]is  [Orissa JEE 2002]

A)            \[{{x}^{2}}+{{y}^{2}}-2xy-4x+4y-4=0\]

B)            \[{{x}^{2}}+{{y}^{2}}-2xy+4x-4y-4=0\]

C)            \[{{x}^{2}}+{{y}^{2}}+2xy-4x+4y-4=0\]

D)            \[{{x}^{2}}+{{y}^{2}}+2xy-4x-4y+4=0\]

Correct Answer: C

Solution :

           Let focus is \[S(0,\,0)\] and A is the vertex of parabola. Take any point Z such that AS = AZ. Given tangent at vertex is \[x-y+1=0.\]            Since directrix is parallel to the tangent at the vertex.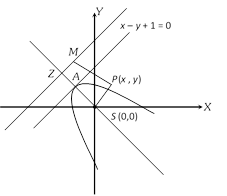                   \[\therefore \] Equation of directrix is \[x-y+\lambda =0\], where \[\lambda \] is constant.            \[\because \] A is midpoint of SZ,  \[\therefore \] SZ = 2.SA            Þ\[\frac{|0-0+\lambda |}{\sqrt{{{1}^{2}}+{{(-1)}^{2}}}}=2\times \frac{|0-0+1|}{\sqrt{{{1}^{2}}+{{(-1)}^{2}}}}\]Þ\[|\lambda |\,=2\]  i.e. \[\lambda =2\]            \[\because \] Directrix in this case always lies in IInd quadrant            \ \[\lambda =2\]            Hence equation of directrix is \[x-y+2=0\]            Now, P be any point on parabola            \ SP = PM Þ \[S{{P}^{2}}=P{{M}^{2}}\]            Þ \[{{(x-0)}^{2}}+{{(y-0)}^{2}}={{\left( \frac{|x-y+2|}{\sqrt{2}} \right)}^{2}}\]                    Þ \[{{x}^{2}}+{{y}^{2}}+2xy-4x+4y-4=0.\]