question_answer

If the complex number \[{{z}_{1}},{{z}_{2}}\] the origin form an equilateral triangle then  \[z_{1}^{2}+z_{2}^{2}=\] [IIT 1983]

A) \[{{z}_{1}}\,{{z}_{2}}\]

B)  \[{{z}_{1}}\,\overline{{{z}_{2}}}\]

C) \[\overline{{{z}_{2}}}\,{{z}_{1}}\]

D) \[|{{z}_{1}}{{|}^{2}}=|{{z}_{2}}{{|}^{2}}\]

Correct Answer: A

Solution :

Let \[OA,OB\] be the sides of an equilateral \[\Delta OAB\]and let \[OA,OB\]represent the complex numbers or vectors  \[{{z}_{1}},\,{{z}_{2}}\] respectively.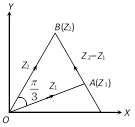 From the equilateral \[\Delta OAB,\overrightarrow{AB}={{z}_{2}}-{{z}_{1}}\] \[\therefore \]  \[arg\,\,\left( \frac{{{z}_{2}}-{{z}_{1}}}{{{z}_{2}}} \right)=arg\,({{z}_{2}}-{{z}_{1}})-arg\,{{z}_{2}}=\pi /3\] and\[arg\left( \frac{{{z}_{2}}}{{{z}_{1}}} \right)=arg({{z}_{2}})-arg({{z}_{1}})=\frac{\pi }{3}\] Also\[\left| \frac{{{z}_{2}}-{{z}_{1}}}{{{z}_{2}}} \right|=1=\left| \frac{{{z}_{2}}}{{{z}_{1}}} \right|\], since triangle is equilateral. Thus the vectors \[\frac{{{z}_{2}}-{{z}_{1}}}{{{z}_{2}}}\]and \[\frac{{{z}_{2}}}{{{z}_{1}}}\] have same modulus and same argument, which implies that the vectors are equal, that is  \[\frac{{{z}_{2}}-{{z}_{1}}}{{{z}_{2}}}=\frac{{{z}_{2}}}{{{z}_{1}}}\]Þ\[{{z}_{1}}{{z}_{2}}-z_{1}^{2}=z_{2}^{2}\]Þ\[z_{1}^{2}+z_{2}^{2}={{z}_{1}}{{z}_{2}}\] Note: Students should remember this question as a formula.