-
question_answer1)
Two trains A and B are running in the same direction on parallel tracks such that A is faster than B. If packets of equal weight are exchanged between the two, then
A)
A will be retarded but B will be accelerated done
clear
B)
A will be accelerated but B will be retarded done
clear
C)
there will be no change in velocity of A but B will be accelerated done
clear
D)
there will be no change in velocity of B, but A will be accelerated done
clear
View Solution play_arrow
-
question_answer2)
A perfectly straight portion of a uniform rope has mass M and length L. At end A of the segment, the tension in the rope is \[{{T}_{A}}\] and at end B it is \[{{T}_{B}}({{T}_{B}}>{{T}_{A}})\]. Neglect effect of gravity and no contact force acts on the rope in between points A and B. The tension in the rope at a distance L/5 from end A is
A)
\[{{T}_{B}}-{{T}_{A}}\] done
clear
B)
\[({{T}_{A}}+{{T}_{B}})/5\] done
clear
C)
\[(4{{T}_{A}}+{{T}_{B}})/5\] done
clear
D)
\[({{T}_{A}}-{{T}_{B}})/5\] done
clear
View Solution play_arrow
-
question_answer3)
In the arrangement shown in figure the ends P and Q of an stretchable string move downwards with a uniform speed U. Pulleys A and B are fixed. Mass M moves upwards with a speed of
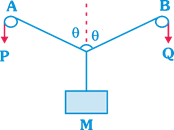
A)
\[2U\cos \theta \] done
clear
B)
\[U\cos \theta \] done
clear
C)
\[2U/\cos \theta \] done
clear
D)
\[U/\cos \theta \] done
clear
View Solution play_arrow
-
question_answer4)
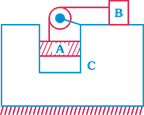
In the system shown in figure \[{{m}_{A}}=4m,\,\,{{m}_{B}}=3m\] and \[{{m}_{C}}=8m\]. Friction is absent everywhere. String is light and inextensible. If the system is released from rest find the acceleration of block B
A)
\[\frac{g}{8}\] done
clear
B)
\[\frac{g}{2}\] done
clear
C)
\[\frac{g}{4}\] done
clear
D)
g done
clear
View Solution play_arrow
-
question_answer5)
If a man throws up a ball and catches it after some time, this time is called time of flight. Time of flight in these types of motion depend on whether the man is stationary or he is accelerated. If the man is in a moving lift throws a ball and catches it after time \[{{t}_{1}}\] when lift is moving up with acceleration a and catches the ball in time \[{{t}_{2}}\] if the lift is moving down with same acceleration a. The speed with which ball is thrown w.r.t. man -
A)
\[\frac{g{{t}_{1}}{{t}_{2}}}{{{t}_{1}}-{{t}_{2}}}\] done
clear
B)
\[\frac{g{{t}_{1}}{{t}_{2}}}{{{t}_{1}}+{{t}_{2}}}\] done
clear
C)
\[\frac{2g{{t}_{1}}{{t}_{2}}}{{{t}_{1}}-{{t}_{2}}}\] done
clear
D)
\[\frac{2g{{t}_{1}}{{t}_{2}}}{{{t}_{1}}+{{t}_{2}}}\] done
clear
View Solution play_arrow
-
question_answer6)
A toy train consists of three identical compartment A, B and C. It is being pulled by a constant force F along C. The ratio of the tensions in the string connecting AB and BC is:
A)
2 : 1 done
clear
B)
1 : 3 done
clear
C)
1 : 1 done
clear
D)
1 : 2 done
clear
View Solution play_arrow
-
question_answer7)
Two blocks of masses \[{{m}_{1}}\] and \[{{m}_{2}}\] are placed in contact with each other on a horizontal platform. The coefficient of friction between the platform and the two blocks is the same. The platform moves with an acceleration. The force of interaction between the blocks is

A)
zero, only if \[{{m}_{1}}={{m}_{2}}\] done
clear
B)
non-zero, when \[{{m}_{1}}>{{m}_{2}}\] done
clear
C)
non-zero, when \[{{m}_{1}}<{{m}_{2}}\] done
clear
D)
zero in all cases done
clear
View Solution play_arrow
-
question_answer8)
If \[F=20\text{ }N,\] with how much force does block A presses the block B -
A)
10 N done
clear
B)
20 N done
clear
C)
30 N done
clear
D)
Zero done
clear
View Solution play_arrow
-
question_answer9)
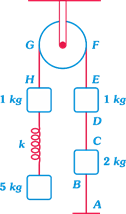
In the situation shown in the figure, the system is in equilibrium. All the strings, spring and pulley are light. Just after cutting the string AB,
A)
the tension in the string GH is 6 g done
clear
B)
the tension in the string GH is zero done
clear
C)
the tension in string GH is \[\frac{21}{4}g\] done
clear
D)
the 2 kg block remains in equilibrium done
clear
View Solution play_arrow
-
question_answer10)
If M is mass of rocket, r is rate of ejection of gases with respect to rocket, then acceleration of the rocket \[\frac{dv}{dt}\] is equal to
A)
\[\frac{ru}{(m-rt)}\] done
clear
B)
\[\frac{(m-rt)}{ru}\] done
clear
C)
\[\frac{ru}{(m+rt)}\] done
clear
D)
\[\frac{ru}{m}\] done
clear
View Solution play_arrow
-
question_answer11)
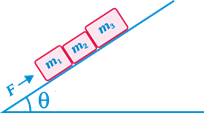
Three blocks are placed at rest on a smooth inclined plane with force acting on \[{{m}_{1}}\] parallel to the inclined plane. Find the contact force between \[{{m}_{2}}\] and \[{{m}_{3}}\]:
A)
\[\frac{({{m}_{1}}+{{m}_{2}}+{{m}_{3}})F}{{{m}_{3}}}\] done
clear
B)
\[\frac{{{m}_{3}}F}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\] done
clear
C)
\[F-({{m}_{1}}+{{m}_{2}})g\] done
clear
D)
F done
clear
View Solution play_arrow
-
question_answer12)
A truck moving on a smooth horizontal surface with a uniform speed u is carrying dust. If a mass \[\Delta m\] of the dust leaks from the truck in vertical downward direction in time \[\Delta t,\] the force needed to keep the truck moving at its constant speed is
A)
Zero done
clear
B)
\[\frac{u\,\Delta m}{\Delta t}\] done
clear
C)
\[\Delta m\times \frac{du}{dt}\] done
clear
D)
\[u\frac{\Delta m}{\Delta t}+\Delta m\times \frac{du}{dt}\] done
clear
View Solution play_arrow
-
question_answer13)
An object is kept on a smooth inclined plane of 1 in \[l\]. The horizontal acceleration to be imparted to the inclined plane so that object is stationary relative to the incline is given by
A)
\[g({{l}^{2}}-1)\] done
clear
B)
\[g({{l}^{2}}-1)\] done
clear
C)
\[\frac{g}{\sqrt{{{l}^{2}}-1}}\] done
clear
D)
\[\frac{g}{{{l}^{2}}-l}\] done
clear
View Solution play_arrow
-
question_answer14)
Two men of masses m and m/2 starts climbing up on two massless strings fixed at the ceiling with acceleration g and g/2 respectively. The ratio of tensions in the two strings will be:
A)
2 : 1 done
clear
B)
4 : 1 done
clear
C)
4 : 3 done
clear
D)
8 : 3 done
clear
View Solution play_arrow
-
question_answer15)
A body of mass m released from a height h on a smooth inclined plane that is shown in the figure. The following can be true about the velocity of the block knowing that the wedge is fixed.

A)
v is maximum when it just touches the spring done
clear
B)
v is maximum when it compresses the spring by some amount done
clear
C)
v is maximum when the spring comes back to natural position done
clear
D)
none of these done
clear
View Solution play_arrow
-
question_answer16)
Two solid rubber balls A and B having masses 200 and 400 gm respectively are moving in opposite directions with velocity of A equal to 0.3 m/s. After collision the two balls come to rest, then the velocity of B is:
A)
0.15 m/s done
clear
B)
1.5 m/s done
clear
C)
- 0.15 m/s done
clear
D)
None of the above done
clear
View Solution play_arrow
-
question_answer17)
A body of mass 3kg is acted on by a force which varies as shown in the graph below The momentum acquired is given by
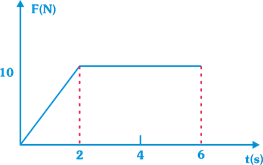
A)
Zero done
clear
B)
5 N-s done
clear
C)
30 N-s done
clear
D)
50 N-s done
clear
View Solution play_arrow
-
question_answer18)
Two masses \[{{m}_{1}}\] and \[{{m}_{2}}\] which are connected with a light string, are placed over a frictionless pulley. This set up is placed over a weighing machine, as shown. Three combination of masses \[{{m}_{1}}\] and \[{{m}_{2}}\] are used, in first case \[{{m}_{1}}=6\,kg\] and \[{{m}_{2}}=2\,kg,\] in second case \[{{m}_{1}}=5\,kg\] and \[{{m}_{2}}=3\,kg\] and in third case \[{{m}_{1}}=4\,kg\] and \[{{m}_{2}}=4\,kg\]. Masses are held stationary initially and then released. If the readings of the weighing machine after the release in three cases are\[{{W}_{1}},\,{{W}_{2}}\] and \[{{W}_{3}}\] respectively then:
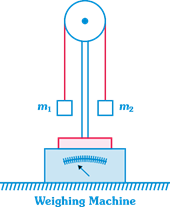
A)
\[{{W}_{1}}>{{W}_{2}}>{{W}_{3}}\] done
clear
B)
\[{{W}_{1}}<{{W}_{2}}<{{W}_{3}}\] done
clear
C)
\[{{W}_{1}}={{W}_{2}}={{W}_{3}}\] done
clear
D)
\[{{W}_{1}}={{W}_{2}}<{{W}_{3}}\] done
clear
View Solution play_arrow
-
question_answer19)
A light spring of length I and spring constant k is placed vertically on a table. A small ball of mass m falls on it. The height h from the surface of the table at which the ball will have the maximum velocity is
A)
\[\frac{l}{k}\] done
clear
B)
\[l-\frac{mg}{k}\] done
clear
C)
\[l+\frac{k}{mg}\] done
clear
D)
\[l-kg\] done
clear
View Solution play_arrow
-
question_answer20)
A metal sphere is hung by a string fixed to a wall. The forces acting on the sphere are shown in figure. Which of following statements are correct:
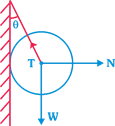
A)
\[\overrightarrow{N}+\overrightarrow{T}+\overrightarrow{W}=0\] done
clear
B)
\[{{T}^{2}}+{{N}^{2}}+{{W}^{2}}=0\] done
clear
C)
\[T=N+W\] done
clear
D)
\[N=W\sin \theta \] done
clear
View Solution play_arrow
-
question_answer21)
| A body of mass 50 kg resting on a smooth inclined plane is connected by a massless inextensible string passing over a smooth pulley, at the top of the inclined plane have another mass of 40 kg as shown in the figure. The distance through which 50 kg mass fall in 4 sec will be - |
| (The angle of the inclined plane is \[{{30}^{o}}\]) |
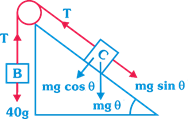 |
A)
13.04 m done
clear
B)
1.63 m done
clear
C)
1.304 m done
clear
D)
16.3 m done
clear
View Solution play_arrow
-
question_answer22)
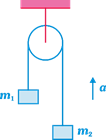
The figure shows a pulley mass system which is kept in an elevator moving up with acceleration g. Then the tension T in the string is given by
A)
\[\frac{{{m}_{1}}{{m}_{2}}g}{{{m}_{1}}+{{m}_{2}}}\] done
clear
B)
\[\frac{2{{m}_{1}}{{m}_{2}}g}{{{m}_{1}}+{{m}_{2}}}\] done
clear
C)
\[\frac{4{{m}_{1}}{{m}_{2}}g}{{{m}_{1}}+{{m}_{2}}}\] done
clear
D)
\[\frac{({{m}_{1}}-{{m}_{2}})g}{{{m}_{1}}+{{m}_{2}}}\] done
clear
View Solution play_arrow
-
question_answer23)
The system shown in figure 18 is in equilibrium. The maximum value of W, so that the maximum value of static frictional force on 100 kg body is 450 N, will be

A)
100 N done
clear
B)
250 N done
clear
C)
450 N done
clear
D)
1000 N done
clear
View Solution play_arrow
-
question_answer24)
A man stands on a weighing machine kept inside a lift. Initially the lift is ascending with the acceleration 'a' due to which the reading is W. Now the lift decends with the same acceleration and reading is 10% of initial. Find the acceleration of lift?
A)
\[\frac{g}{19}\,m/{{\sec }^{2}}\] done
clear
B)
\[\frac{9g}{11}\,m/{{\sec }^{2}}\] done
clear
C)
\[0\,/{{\sec }^{2}}\] done
clear
D)
\[g\,m/{{\sec }^{2}}\] done
clear
View Solution play_arrow
-
question_answer25)
Choose the correct option.
A)
Law and inertia and Newton's 1st law are same done
clear
B)
Conservation of momentum is a consequence of Newton's 3rd law done
clear
C)
Both [a] and [b] are correct done
clear
D)
Both [a] and [b] are wrong done
clear
View Solution play_arrow
-
question_answer26)
A spring is compressed between blocks of masses \[{{m}_{1}}\] and \[{{m}_{2}}\] placed on a smooth horizontal surface as shown in the figure. When the blocks are release, they have initial velocity of \[{{v}_{1}}\] and \[{{v}_{2}}\] in the direction shown. The blocks travel distances \[{{x}_{1}}\] and \[{{x}_{2}}\] before coming to rest. The ratio of \[\frac{{{x}_{1}}}{{{x}_{2}}}\] is

A)
\[\frac{{{m}_{1}}}{{{m}_{2}}}\] done
clear
B)
\[\sqrt{\frac{{{m}_{1}}}{{{m}_{2}}}}\] done
clear
C)
\[\frac{{{m}_{2}}}{{{m}_{1}}}\] done
clear
D)
\[\sqrt{\frac{{{m}_{2}}}{{{m}_{1}}}}\] done
clear
View Solution play_arrow
-
question_answer27)
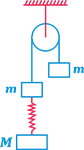
The system shown in figure is released from rest. The spring gets elongated
A)
for M > m done
clear
B)
for M > 2 m done
clear
C)
for \[M>\frac{m}{2}\] done
clear
D)
for any value of M done
clear
View Solution play_arrow
-
question_answer28)
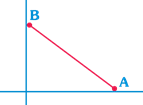
Two particles A and B are connected by a rigid rod AB. The rod slides along perpendicular rails as shown here. The velocity of A to the left is 10 m/s. What is the speed of B when angle \[\theta ={{45}^{o}}?\]
A)
5 m/s done
clear
B)
(b)\[5\sqrt{2}m/s\] done
clear
C)
10 m/s done
clear
D)
7.5 m/s done
clear
View Solution play_arrow
-
question_answer29)
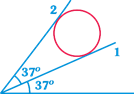
A sphere of mass m is held between two smooth inclined walls. For sin \[37{}^\circ =3/5,\] the normal reaction of the wall (2) is equal to :
A)
mg done
clear
B)
\[mg\sin {{74}^{o}}\] done
clear
C)
\[mg\cos {{74}^{o}}\] done
clear
D)
none of the above done
clear
View Solution play_arrow
-
question_answer30)
An explosion blows a rock into three parts. Two parts go off at right angles of each other. These two are 1 kg first part moving with a velocity of \[12\,m{{s}^{-1}}\] and 2 kg second part moving with a velocity of \[8\,m{{s}^{-1}}\]. If the third part files off with a velocity of \[4\,m{{s}^{-1}},\] its mass would be :
A)
5 kg done
clear
B)
7 kg done
clear
C)
17 kg done
clear
D)
3 kg done
clear
View Solution play_arrow
-
question_answer31)
A balloon with mass M is descending down with an acceleration a (a < g). What mass' of its contents must be removed so that it starts moving up with same acceleration a
A)
\[\frac{2M\left( g \right)}{a}\] done
clear
B)
\[\frac{M\left( g+a \right)}{g}\] done
clear
C)
\[\frac{Mg}{g+a}\] done
clear
D)
\[\frac{2Ma}{g+a}\] done
clear
View Solution play_arrow
-
question_answer32)
A particle moves in the \[x-y\] plane under the action of a force \[\overrightarrow{F}\] such that the value of its linear momentum \[\overrightarrow{P}\] at any time \[t\] is \[{{P}_{x}}=2\,\cos t,\] \[{{P}_{y}}=2\sin t\]. The angle \[\theta \] between \[\overrightarrow{F}\] and \[\overrightarrow{P}\] at a given time t will be
A)
\[90{}^\circ \] done
clear
B)
\[0{}^\circ \] done
clear
C)
\[180{}^\circ \] done
clear
D)
\[30{}^\circ \] done
clear
View Solution play_arrow
-
question_answer33)
| Two masses\[{{\text{m}}_{1}}\]and\[{{\text{m}}_{\text{2}}}\]are attached to the ends of a massless string which passes over a frictionless pulley attached to the top of an inclined plane. The angle of inclination of the plane is \[\theta \]. Take \[g=10m{{s}^{-2}}\] |
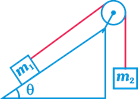 |
| If \[{{m}_{1}}=10\,kg,\,\,{{m}_{2}}=5\,kg,\] \[\theta ={{30}^{o}},\] what is the acceleration of mass \[{{m}_{2}}\]? |
A)
zero done
clear
B)
\[(2/3)\text{ }m{{s}^{-2}}\] done
clear
C)
\[5\text{ }m{{s}^{-2}}\] done
clear
D)
\[10/3\text{ }m{{s}^{-2}}\] done
clear
View Solution play_arrow
-
question_answer34)
A block of mass M is pulled along a horizontal frictionless surface by a rope of mass m. If a force P is applied at the free end of the rope, the force exerted by the rope on the block is
A)
\[\frac{PM}{M+m}\] done
clear
B)
\[\frac{Pm}{M+m}\] done
clear
C)
\[\frac{Pm}{M-m}\] done
clear
D)
P done
clear
View Solution play_arrow
-
question_answer35)
A rocket of initial mass 6000 kg ejects mass at a constant rate of 20 kg/s with constant relative speed of 10 km/s. What is the acceleration of the rocket after 50 second, (Neglect gravity)
A)
\[50\,m/{{s}^{2}}\] done
clear
B)
\[40\,m/{{s}^{2}}\] done
clear
C)
\[60\,m/{{s}^{2}}\] done
clear
D)
30 m/\[\Omega \] done
clear
View Solution play_arrow

