question_answer

A cone of maximum volume is inscribed in a given sphere, then ratio of the height of the cone to diameter of the sphere is [MNR 1985; UPSEAT 2000]

A)            2/3

B)            3/4

C)            1/3

D)            ¼

Correct Answer: A

Solution :

           Let diameter of sphere \[AE=2r\]            Let radius of cone is x and height is y            \ \[AD=y\], since \[B{{D}^{2}}=AD.DE\]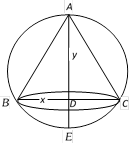            or \[{{x}^{2}}=y(2r-y)\]                                      ??(i)            Volume of cone \[V=\frac{1}{3}\pi {{x}^{2}}y=\frac{1}{3}\pi y(2r-y)y\]                                     \[=\frac{1}{3}\pi (2r{{y}^{2}}-{{y}^{3}})\]            Þ \[\frac{dV}{dy}=\frac{1}{3}\pi (4ry-3{{y}^{2}})\] Þ \[\frac{dV}{dy}=0\]            Þ \[\frac{1}{3}\pi (4ry-3{{y}^{2}})=0\] Þ \[y(4r-3y)=0\]Þ \[y=\frac{4}{3}r,\,0\]            Now \[\frac{{{d}^{2}}V}{d{{y}^{2}}}=\frac{1}{3}\pi (4r-6y)\], put \[y=\frac{4}{3}r\]            Þ  \[\frac{{{d}^{2}}V}{d{{y}^{2}}}=\frac{1}{3}\pi \,\left( 4r-6\times \frac{4}{3}r \right)\] = negative value            So, volume of cone is maximum at \[y=\frac{4}{3}r\]            Þ  \[\frac{\text{Height}}{\text{Diametre}}\]=\[\frac{y}{2r}=\frac{2}{3}\].