question_answer

In \[\Delta OPQ\] right-angled at P, \[OP=7cm,\]and \[OQ-PQ=1cm,\]then the value of \[\sin Q\] is: (NCERT Exercise)

A) \[\frac{3}{25}\]

B) \[\frac{1}{5}\]

C) \[\frac{7}{25}\]

D) \[\frac{9}{25}\]

Correct Answer: C

Solution :

[c] Given, \[\angle P=90{}^\circ \]and \[OP=7\,cm\]

Also,\[OQ-PQ=1cm\] .(1)

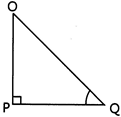In \[\Delta OPQ,\]

\[O{{Q}^{2}}=O{{P}^{2}}+P{{Q}^{2}}\]

\[\Rightarrow \,\,\,\,O{{P}^{2}}=O{{Q}^{2}}-P{{Q}^{2}}\]

\[\Rightarrow \,\,\,\,{{(7)}^{2}}=(OQ+PQ)\,\,(OQ-PQ)\]

\[[{{a}^{2}}-{{b}^{2}}=(a+b)\,\,(a-b)]\]

\[\Rightarrow \,\,\,\,49=(OQ+PQ)\cdot 1\][from eq. (1)]

\[\Rightarrow \,\,\,\,OQ+PQ=49\] ..(2)

From eqs. (1) and (2), we get

\[2OQ=50\,\,\,\,\,\,\,\Rightarrow \,OQ=25cm\]

and \[PQ=49-25=24cm\]

So,\[\sin Q=\frac{OP}{OQ}=\frac{7}{25}\]