question_answer

In the given figure, O is the center of the circle and AB is the diameter of the circle of length 14 cm. Find the area of shaded portion.

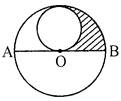
A) \[38.5\,\,c{{m}^{2}}\]         

B) \[9.625\,\,c{{m}^{2}}\]     

C) \[19.25\,\,c{{m}^{2}}\]                   

D)  None of these

Correct Answer: C

Solution :

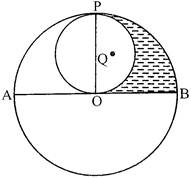\[AB=14\,\,cm\] \[\therefore \]\[AO=OB=7\,\,cm\] \[\therefore \]\[OP=7\,\,cm\] Again, In small circle Radius \[=\frac{7}{2}cm\] \[\therefore \]Area of Semicircle             \[PQO=\frac{1}{2}\times \frac{22}{7}\times \frac{7}{2}\times \frac{7}{2}=\frac{77}{4}c{{m}^{2}}\] Now. Area of sector \[=\frac{\theta }{360{}^\circ }\pi {{r}^{2}}=\frac{90{}^\circ }{360}\times \frac{22}{7}\times 7\times 7=\frac{154}{4}c{{m}^{2}}\] Area of shaded portion \[=\frac{154}{4}-\frac{77}{4}=\frac{77}{4}=19\frac{1}{4}=19.25c{{m}^{2}}\]