A) \[675.714\,c{{m}^{2}}\]
B) \[685.4\,c{{m}^{2}}\]
C) \[695.4\,c{{m}^{2}}\]
D) \[775.4\,c{{m}^{2}}\]
E) None of these
Correct Answer: A
Solution :
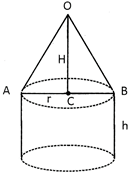
Explanation Option [a] is correct. Note that the radius of the cylinder and the radius of the base of the cone have the same size. We first use the formula of the volume of the cone to find its height H: \[\left( \frac{1}{3} \right)\pi \,5\,\,{{\times }^{2}}h=100\,\,\pi \Rightarrow h=12\,\,cm\] \[{{\ell }^{2}}+{{h}^{2}}+{{r}^{2}}\Rightarrow \ell =13\] The area of lateral surface of the cone and that of the cylinder is added to obtain the total area of the surface. So, lateral surface area of the figure = \[2\pi rh+\pi r\ell =\pi r\left( 2h+\ell \right)\] = \[\frac{22}{7}\times 5\left( 30+13 \right)=675.714\,c{{m}^{2}}\]You need to login to perform this action.
You will be redirected in
3 sec
