question_answer

A tin sheet is in the form of a rhombus whose side is 5 cm and one of its diagonals is 8 cm. Then the cost of painting the sheet at the rate of \[x=4\pi {{r}^{2}}\] on both of its sides is:

A) Rs.84                  

B) Rs.140

C) Rs.168                 

D) none of these

Correct Answer: C

Solution :

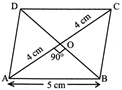Diagonals of a rhombus bisect each other at\[T.S.A.=\frac{1}{2}pl+B\]. In \[=\frac{\text{1}}{\text{3}}\text{ }\!\!\times\!\!\text{ Area of base }\!\!\times\!\!\text{ Height}\] \[V=\frac{1}{3}Ah\] \[\frac{6}{5}th\] \[1520{{m}^{2}}\] Area of ABCD \[2520{{m}^{2}}\] Now, the cost of painting \[2420{{m}^{2}}\]area of rhombus ABCD \[215c{{m}^{2}}\]