A) \[{{\tan }^{-1}}({{t}^{2}})\]
B) \[{{\cot }^{-1}}({{t}^{2}})\]
C) \[{{\tan }^{-1}}(t)\]
D) \[{{\cot }^{-1}}(t)\]
Correct Answer: C
Solution :
[c] Tangent and normal at \[P(a{{t}^{2}},2at)\]to the parabola \[{{y}^{2}}=4ax\]are, respectively, \[ty=x+a{{t}^{2}}\] \[and\,\,y=-tx+2at+a{{t}^{3}}\] Equations (i) and (ii) meet the x-axis where y=0. From (i), \[x=-a{{t}^{2}}\] Therefore, T is \[(-a{{t}^{2}},0)\]. Form (ii), \[tx=2at+a{{t}^{3}}\]. Therefore, G is \[(2a+a{{t}^{3}},0).\] Midpoint of TG= \[=\left( \frac{2a+a{{t}^{2}}-a{{t}^{2}}}{2} \right)\equiv 0(a,0)\] Since\[\angle TPG=90{}^\circ \], the center of the circle through PTG is (a, 0). If \[\theta \]is the angle between tangents at P to the parabola and circle through P, T and G then \[(90{}^\circ -\theta )\]is the angle between PT and OP. Slope of PT=\[\frac{2at}{2a{{t}^{2}}}=\frac{1}{t}\] Slope of OP\[=\frac{2at}{a({{t}^{2}}-1)}=\frac{2t}{{{r}^{2}}-1}\] \[\therefore \tan (90{}^\circ -\theta )=\left| \frac{\frac{1}{t}-\frac{2t}{{{r}^{2}}-1}}{1+\frac{1}{t}\left( \frac{2t}{{{r}^{2}}-1} \right)} \right|=\frac{1}{t}\] \[\therefore \cot \theta =\frac{1}{t}\] Or \[\tan \theta =t\] Or \[\theta ={{\tan }^{-1}}(t)\]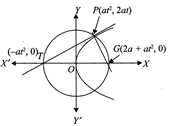
You need to login to perform this action.
You will be redirected in
3 sec
