question_answer

Two polaroids are placed in the path of unpolarized beam of intensity \[{{I}_{0}}\] such that no light is emitted from the second polaroid. If a third polaroid whose polarization axis makes an angle q with the polarization axis of first polaroid, is placed between these polaroids then the intensity of light emerging from the last polaroid will be           [UPSEAT 2005]

A)            \[\left( \frac{{{I}_{0}}}{8} \right){{\sin }^{2}}2\theta \]        

B)            \[\left( \frac{{{I}_{0}}}{4} \right){{\sin }^{2}}2\theta \]

C)            \[\left( \frac{{{I}_{0}}}{2} \right){{\cos }^{4}}\theta \]         

D)            \[{{I}_{0}}{{\cos }^{4}}\theta \]

Correct Answer: A

Solution :

                   No light is emitted from the second polaroid, so \[{{P}_{1}}\] and \[{{P}_{2}}\] are perpendicular to each other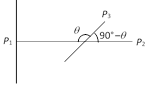                        Let the initial intensity of light is \[{{I}_{0}}\]. So Intensity of light after transmission from first polaroid = \[\frac{{{I}_{0}}}{2}\].            Intensity of light emitted from \[{{P}_{3}}\]  \[{{I}_{1}}=\frac{{{I}_{0}}}{2}{{\cos }^{2}}\theta \]            Intensity of light transmitted from last polaroid i.e. from \[{{P}_{2}}={{I}_{1}}{{\cos }^{2}}({{90}^{o}}-\theta )\]= \[\frac{{{I}_{0}}}{2}{{\cos }^{2}}\theta .{{\sin }^{2}}\theta \]                 \[=\frac{{{I}_{0}}}{8}\]\[{{(2\sin \theta \cos \theta )}^{2}}\]= \[\frac{{{I}_{0}}}{8}{{\sin }^{2}}2\theta \].