question_answer

If AB is a double ordinate of the hyperbola \[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=1\] such that \[\Delta OAB\] is an equilateral triangle O being the origin, then the eccentricity of the hyperbola satisfies.

A) \[e>\sqrt{3}\]

B) \[1<e<\frac{2}{\sqrt{3}}\]

C) \[e=\frac{2}{\sqrt{3}}\]

D) \[e>\frac{2}{\sqrt{3}}\]

Correct Answer: D

Solution :

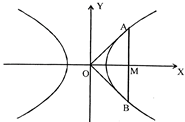
[d] Let the length of the double ordinate be \[2\ell .\]

\[\therefore \,\,\,\,AB=2\ell \] and \[AM=BM=\ell \]

Clearly ordinate of point A is \[\ell \].

The abscissa of the point A is given by

\[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{\ell }^{2}}}{{{b}^{2}}}=1\Rightarrow x=\frac{a\sqrt{{{b}^{2}}+{{\ell }^{2}}}}{b}\]

\[\therefore \] A is \[\left( \frac{a\sqrt{{{b}^{2}}+{{\ell }^{2}}}}{b},\ell  \right)\]

Since \[\Delta OAB\] is equilateral triangle, therefore

\[OA=AB=OB=2\ell .\]

Also, \[O{{M}^{2}}+A{{M}^{2}}=O{{A}^{2}}\]

\[\therefore \frac{{{a}^{2}}({{b}^{2}}+{{\ell }^{2}})}{{{b}^{2}}}+{{\ell }^{2}}=4{{\ell }^{2}}\]

We get \[{{\ell }^{2}}=\frac{{{a}^{2}}{{b}^{2}}}{3{{b}^{2}}-{{a}^{2}}}\]

Since \[{{\ell }^{2}}>0\therefore \frac{{{a}^{2}}{{b}^{2}}}{3{{b}^{2}}-{{a}^{2}}}>0\Rightarrow 3{{b}^{2}}-{{a}^{2}}>0\]

\[\Rightarrow 3{{a}^{2}}({{e}^{2}}-1)-{{a}^{2}}>0\Rightarrow e>\frac{2}{\sqrt{3}}\]