A) 810
B) 540
C) 900
D) 490
Correct Answer: C
Solution :
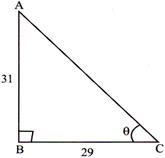
(c) \[29tan\theta =31\Rightarrow tan\theta =\frac{31}{29}\] \[\text{Expression}=\frac{1+2\sin \theta .\cos \theta }{1-2\sin \theta .\cos \theta }\] \[=\frac{{{\sin }^{2}}\theta +{{\cos }^{2}}\theta +2\sin \theta .\cos \theta }{{{\sin }^{2}}\theta +{{\cos }^{2}}\theta -2\sin \theta .\cos \theta }\] \[=\frac{{{\left( \sin \theta +\cos \theta \right)}^{2}}}{{{\left( \sin \theta -\cos \theta \right)}^{2}}}\] \[=\left( \frac{\frac{\sin \theta }{\cos \theta }+\frac{\cos \theta }{\cos \theta }}{\frac{\sin \theta }{\cos \theta }-\frac{\cos \theta }{\cos \theta }} \right)={{\left( \frac{\tan \theta +1}{\tan \theta -1} \right)}^{2}}\] \[={{\left( \frac{\frac{31}{29}+1}{\frac{31}{29}-1} \right)}^{2}}={{\left( \frac{\frac{31+29}{29}}{\frac{31-29}{29}} \right)}^{2}}\] \[={{\left( \frac{60}{2} \right)}^{2}}={{\left( 30 \right)}^{2}}=900\].You need to login to perform this action.
You will be redirected in
3 sec
