question_answer

A rhombus when divided by one diagonal gives two congruent triangles of perimeter 36 cm each. If both the diagonals divide it into 4 congruent triangles of perimeter 24 cm each, what is the side of the rhombus?

A)  10 cm           

B)  11 cm

C)  12 cm           

D)  None of these

Correct Answer: A

Solution :

We know that, perimeter of MBC = 36 cm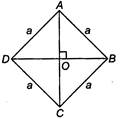   i.e.,          \[a+a+AC=36\] i.e.,            \[2a+2AO=36\] ?(i) Also, perimeter of \[a+AO+BO=24\,cm\] ?(ii) Using Eq. (i), we have \[a+AO=18\] From Eq. (ii),      \[BO=6\,cm\] \[\Rightarrow \] \[BD=12\,cm\] Now, in \[\Delta AOB,\] \[A{{B}^{2}}=A{{O}^{2}}+O{{B}^{2}}\] \[A{{B}^{2}}-A{{O}^{2}}=36\] \[\Rightarrow \] \[(AB-AO)=2\] i.e., \[a-AO=2\] ?(iii) On solving Eqs. (i) and (ii), we get a = 10 = Side of rhombus