question_answer

Rectangular block B, having height h and width d has been placed on another block A as shown in the figure. Both blocks have equal mass and there is no friction between A and the horizontal surface. A horizontal time dependent force \[F=kt\]is applied on the block A. At what time will block B topple? Assume that friction between the two blocks is large enough to prevent B from slipping.

A) \[\frac{dgm}{2kh}\]       

B)        \[\frac{2dgm}{kh}\]

C) \[\frac{dgm}{kh}\]         

D)        \[\frac{3dgm}{2kh}\]

Correct Answer: B

Solution :

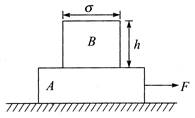
[b] Acceleration \[a=\frac{F}{2m}=\frac{kt}{2m}\] The force diagram of block B in reference frame attached to A is shown in figure. The normal force passes through left edge at the instant the block is about to topple.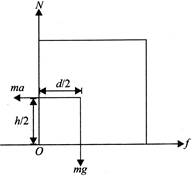 The block will be on verge of toppling when \[ma\frac{h}{2}=mg\frac{d}{2}\] \[m\frac{kt}{2m}\frac{h}{2}=mg\frac{d}{2}\]                 \[\therefore \,\,\,\,t=\frac{2dgm}{kh}\]