A) \[\frac{\pi {{\varepsilon }_{0}}R_{1}^{2}R_{2}^{2}{{V}^{2}}}{{{d}^{2}}{{({{R}_{1}}+{{R}_{2}})}^{2}}}\]
B) \[\frac{\pi {{\varepsilon }_{0}}R_{1}^{2}R_{2}^{2}{{V}^{2}}}{4{{d}^{2}}{{({{R}_{1}}+{{R}_{2}})}^{2}}}\]
C) \[\frac{4\pi {{\varepsilon }_{0}}R_{1}^{2}R_{2}^{2}{{V}^{2}}}{{{d}^{2}}{{({{R}_{1}}+{{R}_{2}})}^{2}}}\]
D) \[\frac{2\pi {{\varepsilon }_{0}}R_{1}^{2}R_{2}^{2}{{V}^{2}}}{{{d}^{2}}{{({{R}_{1}}+{{R}_{2}})}^{2}}}\]
Correct Answer: C
Solution :
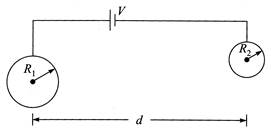
[c] Let's first calculate the capacitance of the system. Assuming that the two spheres have charges Q and \[-Q,\]we can write their potentials as \[{{V}_{1}}=\frac{KQ}{{{R}_{1}}}\] and \[{{V}_{2}}=\frac{K(-Q)}{{{R}_{2}}}\] Note that charge on one sphere does not have any significant effect on the potential of other since \[d>>{{R}_{1}}\]and \[{{R}_{2}}\]. \[\therefore \] Potential difference between the two spheres \[V={{V}_{1}}-{{V}_{2}}=\frac{KQ}{{{R}_{1}}}+\frac{KQ}{{{R}_{2}}}\] \[\therefore \] Capacitance \[C=\frac{Q}{V}=\frac{{{R}_{1}}{{R}_{2}}}{K({{R}_{1}}+{{R}_{2}})}\] Charge on the spheres \[Q=\frac{{{R}_{1}}{{R}_{2}}V}{\left( {{R}_{1}}+{{R}_{2}} \right)}\] \[\therefore \] Force between the spheres \[F=K\frac{{{Q}^{2}}}{{{d}^{2}}}=\frac{K}{{{d}^{2}}}{{\left[ \frac{{{R}_{1}}{{R}_{2}}V}{K({{R}_{1}}+{{R}_{2}})} \right]}^{2}}\] \[=\frac{R_{1}^{2}+R_{2}^{2}{{V}^{2}}}{K{{d}^{2}}{{({{R}_{1}}+{{R}_{2}})}^{2}}}=\frac{4\pi {{\varepsilon }_{0}}R_{1}^{2}R_{2}^{2}{{V}^{2}}}{{{d}^{2}}{{({{R}_{1}}+{{R}_{2}})}^{2}}}\]You need to login to perform this action.
You will be redirected in
3 sec
