question_answer

In the shown circuit, all three capacitor are identical and have capacitance C each. Each resistor has resistance of R. An ideal cell of emf V is connected as shown. Then the potential difference across capacitor \[{{C}_{3}}\] in steady state is:             

A) \[\frac{V}{3}\]                                  

B) \[\frac{V}{2}\]

C) \[\frac{2}{9}V\]                

D) \[\frac{3}{4}V\]

Correct Answer: C

Solution :

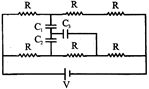
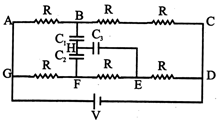The current through branch ABC and GFED in steady state is V/3 R each If we consider \[={{105}^{\text{o}}}\] then \[\vec{V}=(2,\,-1,\,1)\,+\lambda (1,\,2,\,-1)\] and \[\frac{\vec{V}.\vec{r}}{|\vec{r}|}=\frac{4}{\sqrt{6}}\,\Rightarrow \,\,\frac{(\vec{p}.\vec{r})+\lambda (\vec{q}.\vec{r})}{|\vec{r}|}\,=\frac{4}{\sqrt{6}}\] Now the sum of charges on the plates towards point H of the capacitors is zero. \[\therefore \,\frac{-1+\lambda (5)}{\sqrt{6}}\,=\frac{4}{\sqrt{6}}\]\[\therefore \,\,\lambda =1\] \[\therefore \,\,\frac{f(2)-f(0)}{2-0}\,=f'(c)\] Therefore, the p.d. across \[c\in (0,\,2)\] is \[\Rightarrow \,\,\frac{f(2)+3}{2}\le 5\]