question_answer

Hat W contains two white balls and one black ball. Hat B contains two black balls and one white ball. At random, one of the following strategies is selected:  

Two different balls are drawn from hat W.

Two different balls are drawn from hat B.

One ball is drawn from each hat.

The probability of getting at least one white ball, is

A)  \[\frac{1}{2}\]                                  

B)  \[\frac{1}{4}\]

C)  \[\frac{22}{27}\]                                             

D)  \[\frac{21}{27}\]

Correct Answer: C

Solution :

P (atleast) one white ball)             \[=P({{S}_{1}})\,+P({{S}_{2}})\,+P({{S}_{3}})\]                                             ?.(3) Where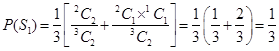    .?(2)             \[P({{S}_{2}})\,=\frac{1}{3}\,\left[ \frac{^{1}{{C}_{1}}\,{{\times }^{2}}{{C}_{1}}}{^{3}{{C}_{2}}} \right]\,=\frac{2}{9}\]                ?(3) and \[P({{S}_{3}})\,=\frac{1}{3}\,\left[ 1-\frac{1}{3}\times \frac{2}{3} \right]\,=\frac{1}{3}\,\left( \frac{7}{9} \right)\,=\frac{7}{27}\,\]        ?(4) \[\therefore \] Using (2), (3) and (4) in (1), we get P(atleast one white ball) \[=\frac{1}{3}\,+\frac{2}{9}\,+\frac{7}{27}\,=\frac{9+6+7}{27}=\frac{22}{27}\]