question_answer

A rectangular coil of single turn, having area A, rotates in a uniform magnetic field B with an angular velocity \[\omega \]about an axis perpendicular to the field. If initially the plane of the coil is perpendicular to the field, then the average induced \[emf\] when it has rotated through \[90{}^\circ \]. is

A)  \[\frac{\omega BA}{\pi }\]             

B)  \[\frac{\omega BA}{2\pi }\]

C) \[\frac{\omega BA}{4\pi }\]               

D)  \[\frac{2\omega BA}{\pi }\]

Correct Answer: D

Solution :

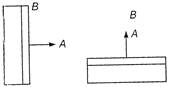  \[\frac{{{T}_{1}}}{{{T}_{2}}}=\frac{15a}{3a}=\frac{5}{1}\] Flux passing through the area of the coil when it is far to magnetic field \[\Rightarrow \] and \[{{T}_{1}}:{{T}_{2}}=5:1\] Flux passing through the area of the coil when it is \[T=M\,\left( g-\frac{g}{4} \right)=\frac{3Mg}{4}\] to the magnetic field \[W=\mathbf{T}\cdot \mathbf{d}\Rightarrow \,W=Td\] \[\Rightarrow \] \[W=-Td=-\frac{3Mgd}{4}\] But       \[\Sigma mvr=\,({{l}_{system}})\omega \] \[\Rightarrow \]            \[mv\frac{l}{2}=\frac{(2m)\,{{(2l)}^{2}}}{12}\omega =\frac{2m(4{{l}^{2}})}{12}\omega \]