question_answer

The minimum value of \[|{{z}_{1}}-{{z}_{2}}|\] and \[{{z}_{1}}\]and\[{{z}_{2}}\] vary over the curve \[|\sqrt{3}\,(1-2z)\,+2i\,|\,=2\sqrt{7}\] and \[|\sqrt{3}\,(-1-z)\,-2i\,|\,=\,|\,\,\sqrt{3}\,(9-z)+18i\,\,|,\] respectively.

A)  \[\frac{7\sqrt{7}}{2\sqrt{3}}\]                     

B)  \[\frac{5\sqrt{7}}{\sqrt{3}}\]

C)  \[\frac{14\sqrt{7}}{\sqrt{3}}\]                     

D)  \[\frac{7\sqrt{7}}{5\sqrt{3}}\]

Correct Answer: B

Solution :

 \[\therefore \] \[F=\frac{1}{r\pi {{\varepsilon }_{0}}}\frac{Q(Q-q)}{{{R}^{2}}}\]      \[\frac{dF}{dq}=0\]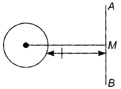 Represents a perpendicular bisector of the line segment joining \[\frac{d}{dq}\,\left[ \frac{Kq(Q-q)}{{{R}^{2}}} \right]=0\]  and \[\Rightarrow \] is \[[Q-2q]=0\] Equation of perpendicular bisector of AB is \[q=\frac{Q}{2}\] \[U=\frac{{{Q}^{2}}}{2C}\]         \[C'=KC\] \[U'=\frac{{{Q}^{2}}}{2C'}=\frac{1}{2}\,\frac{{{Q}^{2}}}{KC}\]   \[\therefore \] \[\frac{U}{U'}=\frac{{{Q}^{2}}/2C}{{{Q}^{2}}/2KC}=K\]   \[{{R}_{\min }}=\frac{r}{n}\] \[{{R}_{\max }}=nr\] Minimum value of \[\therefore \] = Perpendicular distance of centre of circle to the line - Radius of circle \[\frac{{{R}_{\min }}}{{{R}_{\max }}}=\frac{r}{n}\times \frac{1}{nr}=\frac{1}{{{n}^{2}}}\] \[=0.1\times 0.05=5\times {{10}^{-3}}\,{{m}^{2}},\] \[\Delta \phi =-0.05\times {{10}^{-3}}\]