question_answer

The equation of the circle which cuts each of the three circles \[{{x}^{2}}+{{y}^{2}}=4,\]\[{{(x-1)}^{2}}+{{y}^{2}}=4\] and \[{{x}^{2}}+{{(y-2)}^{2}}=4\] orthogonally is

A)  \[{{x}^{2}}+{{y}^{2}}+x+2y+4=0\]

B)  \[{{x}^{2}}+{{y}^{2}}+x-2y+4=0\]

C)  \[{{x}^{2}}+{{y}^{2}}-x-2y+4=0\]

D)  \[{{x}^{2}}+{{y}^{2}}-x+2y+4=0\]

Correct Answer: C

Solution :

 Given,             \[\Rightarrow \] \[[\because |adj\,(adj\,A)|=\,A{{|}^{{{(n-1)}^{2}}}}]\] and                  \[=100\,\left( \frac{\Delta \phi }{\Delta t} \right)\]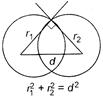 Let the required circle be \[=5\times {{10}^{-3}}\times 100=0.5\,\,V\] Now, by condition of orthoganality,\[R=v\sqrt{\frac{2h}{g}}\]         ?(i) \[u=v,\]            \[u=v+at\]                  ?(ii) and      \[0=v-at\]                   ?(iii) \[\therefore \]    \[-a=\frac{0-v}{t}=-\frac{v}{t}\]      and      \[f=\mu R=\mu mg\] \[a=\mu g\]      \[\therefore \]    [from Eq. (i)] \[t=\frac{v}{a}=\frac{v}{g\mu }\]    \[\eta =\frac{{{P}_{0}}}{{{P}_{i}}}\]       \[\therefore \]    Required equation of circle \[\frac{1}{2}\,m{{v}^{2}}=16\,\,J\] \[v=4\,m{{s}^{-1}}\]