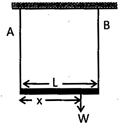
A) L/3
B) L/2
C) \[\frac{2L}{3}\]
D) \[\frac{3L}{4}\]
Correct Answer: C
Solution :
Let tension in wires A & B are \[{{T}_{A}}\And {{T}_{B}}\] respectively.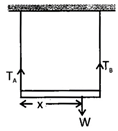 \[{{T}_{A}}+{{T}_{B}}=W\] \[{{T}_{A}}\times x={{T}_{B}}(L-x)\] Solving above equation, \[{{T}_{A}}=\frac{W(L-x)}{L},{{T}_{B}}=\frac{Wx}{L}\] Stress in \[A=\frac{{{T}_{A}}}{{{A}_{A}}}\] where \[{{A}_{A}}\] is CSA of wire A Stress in \[B=\frac{{{T}_{B}}}{{{A}_{B}}}\] where \[{{A}_{B}}\] is CSA of wire B It is given\[{{A}_{A}}=\frac{{{A}_{B}}}{2},\frac{{{T}_{A}}}{{{A}_{A}}}=\frac{{{T}_{B}}}{{{A}_{B}}}\]which gives \[x=\frac{2l}{3}\]
\[{{T}_{A}}+{{T}_{B}}=W\] \[{{T}_{A}}\times x={{T}_{B}}(L-x)\] Solving above equation, \[{{T}_{A}}=\frac{W(L-x)}{L},{{T}_{B}}=\frac{Wx}{L}\] Stress in \[A=\frac{{{T}_{A}}}{{{A}_{A}}}\] where \[{{A}_{A}}\] is CSA of wire A Stress in \[B=\frac{{{T}_{B}}}{{{A}_{B}}}\] where \[{{A}_{B}}\] is CSA of wire B It is given\[{{A}_{A}}=\frac{{{A}_{B}}}{2},\frac{{{T}_{A}}}{{{A}_{A}}}=\frac{{{T}_{B}}}{{{A}_{B}}}\]which gives \[x=\frac{2l}{3}\]
You need to login to perform this action.
You will be redirected in
3 sec
