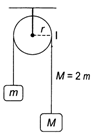
A) \[\sqrt{\frac{2gh}{(M+m){{r}^{2}}+l}}\]
B) \[\sqrt{\frac{2(M+m)gh}{(M-m){{r}^{2}}+l}}\]
C) \[\sqrt{\frac{2Mgh}{(M-m){{r}^{2}}+l}}\]
D) \[\sqrt{\frac{2(M-m)gh}{(M+m){{r}^{2}}+l}}\]
Correct Answer: D
Solution :
Idea In this question as mass moves and pulley rotates then by energy conservation. Loss of potential energy = gain in linear kinetic energy + gain in rotational kinetic energy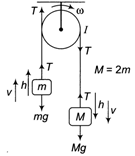 Loss of PE = \[(Mgh-mgh)\] \[=(M-m)gh\] Gain in linear KE\[=\frac{1}{2}(m+M){{v}^{2}}\] Gain in rotational KE\[=\frac{1}{2}l{{\omega }^{2}}\] \[(M-m)gh=\frac{1}{2}(m+M){{v}^{2}}+\frac{1}{2}l{{\omega }^{2}}\] We know\[v=r\omega \] \[(M-m)gh=\frac{1}{2}(m+M){{r}^{2}}{{\omega }^{2}}+\frac{1}{2}l{{\omega }^{2}}\] \[\Rightarrow \]\[{{\omega }^{2}}=\frac{2(M-m)gh}{[(M+m){{r}^{2}}+l]}\] \[\omega =\sqrt{\frac{2(M-m)gh}{(M+m){{r}^{2}}+l}}\] TEST Edge Here, I tangential acceleration of pulley is equal to the I linear acceleration I of two blocks.
Loss of PE = \[(Mgh-mgh)\] \[=(M-m)gh\] Gain in linear KE\[=\frac{1}{2}(m+M){{v}^{2}}\] Gain in rotational KE\[=\frac{1}{2}l{{\omega }^{2}}\] \[(M-m)gh=\frac{1}{2}(m+M){{v}^{2}}+\frac{1}{2}l{{\omega }^{2}}\] We know\[v=r\omega \] \[(M-m)gh=\frac{1}{2}(m+M){{r}^{2}}{{\omega }^{2}}+\frac{1}{2}l{{\omega }^{2}}\] \[\Rightarrow \]\[{{\omega }^{2}}=\frac{2(M-m)gh}{[(M+m){{r}^{2}}+l]}\] \[\omega =\sqrt{\frac{2(M-m)gh}{(M+m){{r}^{2}}+l}}\] TEST Edge Here, I tangential acceleration of pulley is equal to the I linear acceleration I of two blocks. 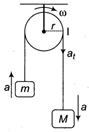
You need to login to perform this action.
You will be redirected in
3 sec
